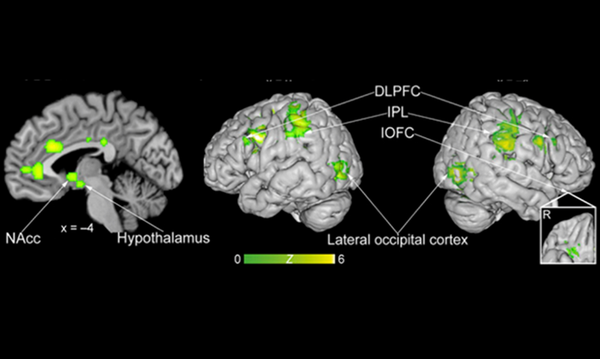
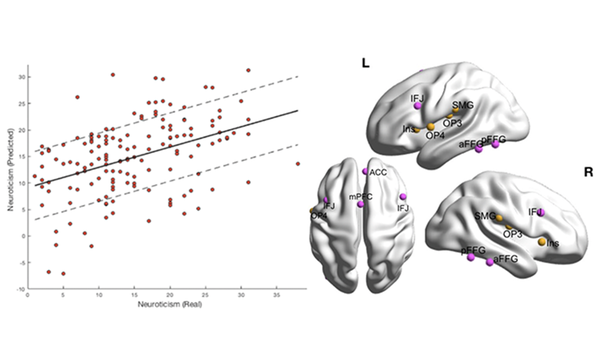
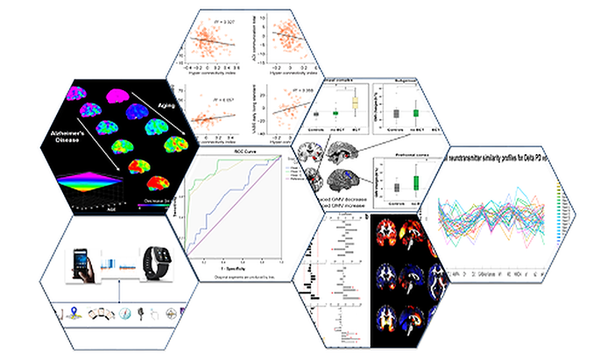
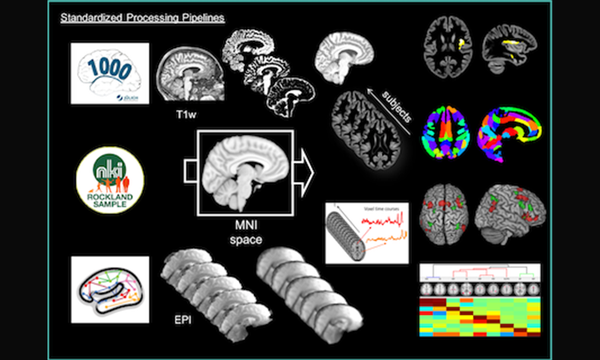
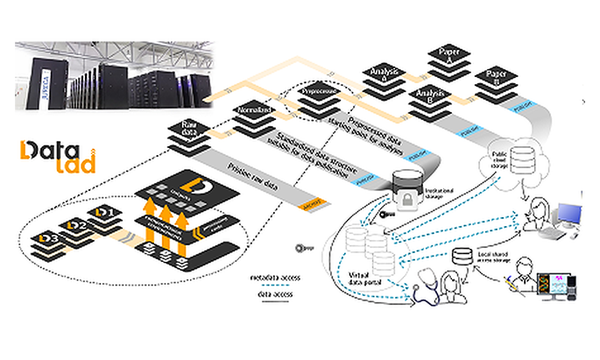
AI all-rounder: ethical, trustworthy, reproducible
To exploit the immense potential of AI responsibly, expertise is required at numerous levels. At our institute, solutions are developed in various groups and interlinked in interdisciplinary projects. The INM-7 is an “AI all-rounder”.