Machine Learning for Quantum Technology
Our research falls into three main categories:
Complex quantum dynamics
Enormous advances in experimental techniques during the past two decades, like the development of quantum simulators of different kinds and ultrafast pump-probe techniques, allow unprecedented control and time-resolved observations of quantum systems with many interacting degrees of freedom.
These developments turned the spotlight on a number of open theoretical questions: Under which conditions and in what sense will a closed system approach a thermal state when prepared far from equilibrium initially? How can the dynamics be characterized on a macroscopic level and what are characteristic time scales? Is there a notion of phases beyond the equilibrium paradigm? We develop and employ computational approaches in order to find answers to such fundamental questions.
An example is the exploration of fluctuations occurring in non-equilibrium processes implemented on a quantum processor: “Quantum Many-Body Jarzynski Equality and Dissipative Noise on a Digital Quantum Computer”, Hahn et al., Phys. Rev. X 13, 041023 (2023).
Neural quantum states
New numerical methods based on the recently introduced neural quantum states (NQS) can potentially allow us to overcome some of the existing limitations, e.g., to simulate non-equilibrium dynamics of two-dimensional systems. The underlying idea is that the proven capabilities of neural networks in pattern recognition and generalization make them well-suited for the representation of many-body wave functions.
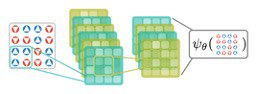
Since neural networks are universal function approximators in the limit of large network sizes, arbitrary quantum states can be represented as NQS in principle. This means that NQS can render variational Monte Carlo techniques numerically exact, which were previously limited by the inductive bias of the chosen ansatz wave functions.
The utility of NQS has been outlined in a number of fundamental works gauging their potential to overcome current limitations of other methods for both low-energy physics and non-equilibrium dynamics. In addition to expressiveness, NQS inherit the neural network’s amenability to leverage le-scale supercomputing resources. Therefore, NQS- based methods can allow us to push the boundaries of classical computing for quantum many-body simulations.
An example is our demonstration that NQS can extend our numerical capabilities when simulating two-dimensional quantum systems far from equilibrium: “Quantum many-body dynamics in two dimensions with artificial neural networks”, Schmitt and Heyl, Phys. Rev. Lett. 125, 100503 (2020).
Reinforcement learning for quantum control
Reinforcement learning (RL) has emerged as one of the central building blocks of modern machine learning for strategy discovery. A pivotal example for the power of this approach is the beating of the world's best human players in complex games like Go or Starcraft with innovative and formerly unknown strategies. RL refers to a family of machine learning algorithms used to train an agent to solve a given task by interacting with an environment through actions and feedback. Importantly, the approach is model-free: information about the behavior of the environment is only gathered through the received response to the actions of the agent.
Moreover, feedback can be incorporated as part of the strategy. These two features distinguish RL from other optimization approaches, and render it a prime candidate to become a core ingredient for the calibration of quantum devices and to discover new quantum-classical algorithms.
An example is our study of RL-based design of elementary quantum gates:
“Reinforcement learning pulses for transmon qubit entangling gates”, Nguyen et al., Mach. Learn.: Science and Technology 5, 025066 (2024).
