Research Areas

Table of Contents

• Associative Memory
• Harnessing analog neuromorphic computing for society’s hardest problems
• Associative Memories, and Computing with Content Addressable Memory (CAM)
• In-memory computing for machine learning inference and training
• Research groups

Associative Memory

Remembering by content, not by address
Biological memory is addressed by content rather than by location: a fragment of a melody, or a glimpse of a partial face, is enough to recall the whole. Conventional computers do the opposite. They retrieve data from explicit numerical addresses and struggle when the input is noisy or incomplete. Building memory that completes patterns and tolerates error is a core primitive for efficient brain-inspired computing, and increasingly for artificial intelligence, since the attention mechanism at the heart of modern language models is itself a form of associative recall.

Associative recall decomposes into three steps: a query is compared against everything stored, one or few entries are selected, and the associated information is returned. Compute-in-memory hardware handles the first and third of these well, because both are matrix operations. The selection between them is not, and is therefore usually displaced into the digital domain, typically as a softmax function, where it becomes the dominant cost of the operation it was meant to conclude. The group addresses this stage from both directions: implementing recall so that comparison and selection happen together inside the array in a single physical step with content addressable memories, and where the selection must be preserved in its original form, realising the softmax function itself as an analog circuit rather than converting every score to digital first. The group designs the memory cell circuits themselves, including gain-cell and memristor-based structures, together with the programming circuitry needed to write analog values reliably into imperfect devices. A key insight is that the precision of such a cell is not set by how many states its device can hold, but by how many comparison boundaries remain distinguishable once temperature, process variation, and read noise are accounted for. Because associative workloads differ in how often their stored content changes, from reference databases written once to attention caches rewritten at every step, the group also organises these cells into memory hierarchies matched to that update frequency.

Analog recall in the age of attention
The group co-developed an analog in-memory attention mechanism for large language models, published in Nature Computational Science (2025), showing that a central operation of modern AI can be executed as associative recall in analog hardware [figure attached below]. Building the underlying primitives that make this possible, the team presented a gain-cell-based analog content-addressable memory for dynamic associative tasks (ISCAS 2025), an analog softmax circuit with wide input current range for compute-in-memory (ISCAS 2025), and a memory-hierarchy design for computing-in-memory (EDTM 2025), and addressed the practical obstacle of device imperfection with a variation-aware analog programming circuit (MetroXRAINE 2024). Earlier work on the non-idealities of analog memristor-based content-addressable memories received the Best Paper Award at NANOARCH 2023. Several of these designs have been filed as patents, indicating a clear route from concept to protected, deployable intellectual property.

Content-addressable memory that tolerates noise underpins pattern recognition, similarity search, and information retrieval, and, as the attention result shows, the operations that dominate modern AI workloads. Implemented in efficient analog hardware, it allows systems to recall and match information where it is already stored, avoiding the data movement that consumes most of the energy in conventional architectures. That an operation can be written as a matrix multiplication is a fact about notation rather than about the operation, and designing hardware for recall rather than for the arithmetic that expresses it opens a design space the arithmetic-first view does not reach. Work continues on scaling these memory arrays and hierarchies while managing device-to-device variability, and on tightening the link between associative hardware and the attention layers of large models, so that the two can co-evolve.

As the demand for more efficient hardware for generative AI has become widely recognised, this direction is now supported by a €2.6 million EXIST-Forschungstransfer grant to develop compute-in-memory hardware for attention, taking the concept from published circuit simulations toward a fabricated hardware system.

Further reading:

Leroux, N., Manea, P.-P., Sudarshan, C., Finkbeiner, J., Siegel, S., Strachan, J. P., & Neftci, E. (2025). Analog in-memory computing attention mechanism for fast and energy-efficient large language models. Nature Computational Science, 5, 544–556. https://doi.org/10.1038/s43588-025-00854-1
Manea, P.-P., Leroux, N., Neftci, E., & Strachan, J. P. (2025). Gain cell-based analog content addressable memory for dynamic associative tasks in AI. 2025 IEEE International Symposium on Circuits and Systems (ISCAS), 1–5. https://doi.org/10.1109/ISCAS56072.2025.11044190
Dube, A., Manea, P.-P., Gibertini, P., Covi, E., & Strachan, J. P. (2025). Analog softmax with wide input current range for in-memory computing. 2025 IEEE International Symposium on Circuits and Systems (ISCAS), 1–5. https://doi.org/10.1109/ISCAS56072.2025.11043251
Manea, P.-P., Sudarshan, C., Cüppers, F., & Strachan, J. P. (2024). Non-idealities and design solutions for analog memristor-based content-addressable memories. Proceedings of the 18th ACM International Symposium on Nanoscale Architectures (NANOARCH '23). https://doi.org/10.1145/3611315.3633254 — Best Paper Award
Yu, J., Manea, P.-P., Ameli, S., Hizzani, M., Eldebiky, A., & Strachan, J. P. (2023). Analog feedback-controlled memristor programming circuit for analog content addressable memory. 2023 IEEE International Conference on Metrology for eXtended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), 983–988. https://doi.org/10.1109/MetroXRAINE58569.2023.10405732

Patents
Manea, P.-P., & Strachan, J. P. (2025). Vorrichtung und Verfahren für eine Ähnlichkeitsbewertung (WO 2025/061322 A1). https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2025061322
Manea, P.-P., & Strachan, J. P. (2024). Schaltkreis für einen CAM (WO 2024/260726 A1). https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2024260726

Software
Manea, P.-P. (2026). torchCAM: A differentiable PyTorch framework for content-addressable memories (Version 0.1.0). https://doi.org/10.5281/zenodo.21718735

Harnessing analog neuromorphic computing for society’s hardest problems

We explore novel approaches to tackle optimization problems, utilizing neuromorphic and physics-inspired principles to solve them faster and more efficiently than traditional CMOS in von Neumann architectures.

Optimization problems are ubiquitous across modern society, needed in training artificial neural networks, constructing optimal schedules (e.g., airlines), path planning (shipping packages, VLSI wire routing), cryptography, drug discovery, and graph analytics (social networks, internet search). These problems are extremely challenging, requiring compute resources that scale exponentially with the problem size (i.e., NP-complete or NP-hard complexity). The research community is even exploring how using quantum computers or quantum-inspired approaches might help us tackle these problems better.

Mathematically, in a combinatorial optimization problem, one has a pre-defined cost function, c(χ) that maps from a discrete domain X(nodes, vectors, graph objects) to ℝ, the real number space, and the goal is to find the χ_opt that achieves the globally optimum cost value c_min( χ_opt) . We explore novel approaches to tackle optimization problems, utilizing neuromorphic and physics-inspired principles to solve them faster and more efficiently than traditional CMOS in von Neumann architectures.

We take a heuristic, rather than exact, approach. There are many powerful heuristic algorithms that have been developed, including simulated annealing, evolutionary algorithms, and Boltzmann machines that apply to many types of optimization problems. A physics-based approach is to map these problems to a Hamiltonian (such as an Ising system), and then find the ground state (lowest energy) of this system. This has inspired hardware development of physics-inspired Ising solvers, and our work is a part of this class.

Heuristic algorithms typically operate by starting with a candidate solution (a guess) and sensing the gradient around the current solution to move toward better ones. The injection of noise is typically required to allow hopping over barriers and avoid getting trapped in local optima. The system then iterates until convergence to a good solution.

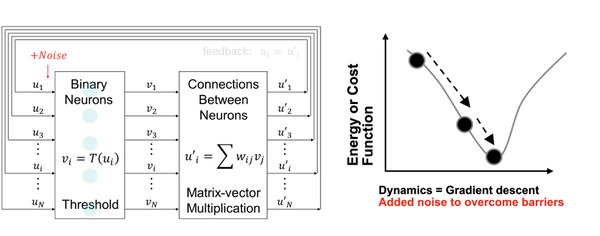
Since the landscape of potential solutions is exponentially large, searching through this space is very costly. Our approach is to 1) offer massive parallelism through many such units operating at once and conducting the search, 2) use in-memory computing to speed-up and reduce the energy of each gradient computation, 3) use analog computing to simultaneously reduce energy, compute faster, and provide a tunable source of very cheap noise. We have built proto-types to showcase all of these ingredients and shown quantitatively the great potential of this approach.

Further reading:

• Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks
• Chaotic dynamics in nanoscale NbO₂ Mott memristors for analogue computing
• Fast Ising solvers based on oscillator networks
• 2021 roadmap on neuromorphic computing and engineering
• Classical Adiabatic Annealing in Memristor Hopfield Neural Networks for Combinatorial Optimization
  

Associative Memories, and Computing with Content Addressable Memory (CAM)

A core part of today’s computing systems are built around memory, specifically data stored perfectly in Random Access Memories (RAM) such as SRAM or DRAM, or longer term in flash drives or hard drives. Yet there is no exactly analogous capability found in biological information processing systems (brains). Instead, “memories” are much more fuzzy, and they don’t allow for easy data fetching (random access) nor perfect recall. Instead, memories are often triggered: an image, a song, a smell, or a taste can kick-off a chain of associated remembrances. The word “associative memory” is used instead in the fields of cognitive science and psychology. While not allowing for random access, these types of memory are still remarkable in many ways: you can feed in a partial, noisy or distorted input (part of a song, perhaps in a new key) and you can recall the original version and even other memories associated with them (where you were, and who you were with, when you first heard this song). Many researchers have strived to develop and understand mathematical models for how such associative memories could work, such as the development of Hopfield networks, holographic memories, correlograms, etc. A key question is: why didn’t biology evolve perfect memories, like RAM? Could there be energetic and information processing advantages to building computing systems around associative memories rather than RAMs? For certain types of computations, we think the answer is yes.

Within electrical engineering and information technology, a type of associative memory has been developed called a Content Addressable Memory (CAM). CAM circuits allow input data to be rapidly searched for any match within the memory. If a match is found, the resulting location is output. This acts almost exactly the opposite to a RAM, where the input is an address and the output is the contents.

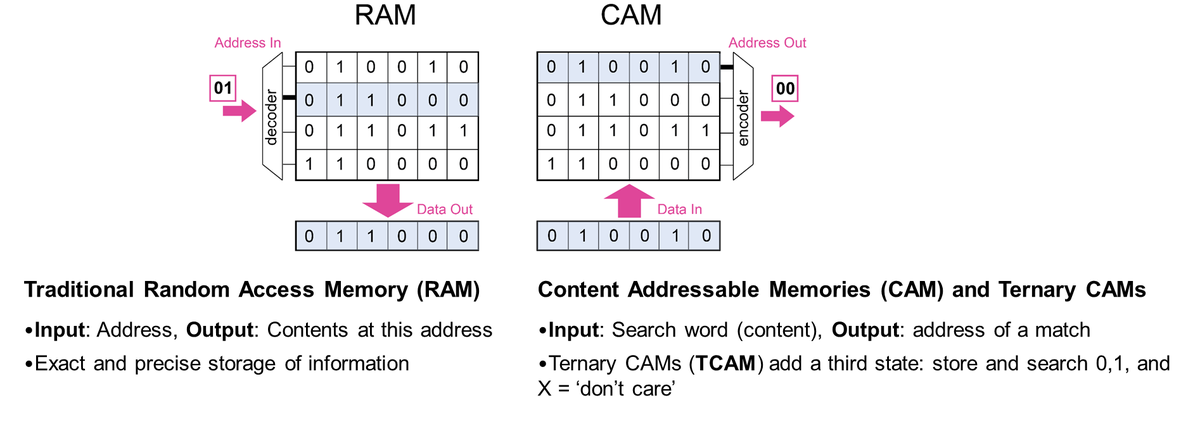
Using such circuit CAMs as part of a computing system rather than a memory system, my team has explored applications that could benefit. This turns out to include important areas in machine learning, security, genomics, and scientific computing. An important example is the broad area of Finite Automata (FA), which are used for regular expression matching with critical applications in the fields of security and genomics. FA are state machines with a set of character inputs, states, and state-transition rules (see below). These can be equivalently encoded into a table called a state transition table. Looking up your current state and current input string within this table then instructs you on which state to go to next, and the procedure is repeated until hitting acceptance or rejection states. The lookup operations in traditional hardware can be very costly and slow, and mapping this instead to a CAM can speed things up tremendously.

Our team has used this insight to build prototype chips to accelerate regular expression matching in the lab. One of the essential ingredients is to replace traditional SRAM-based CAM circuits with new approaches that use the non-volatility and flexibility of memristive devices (“mTCAM cell” below).

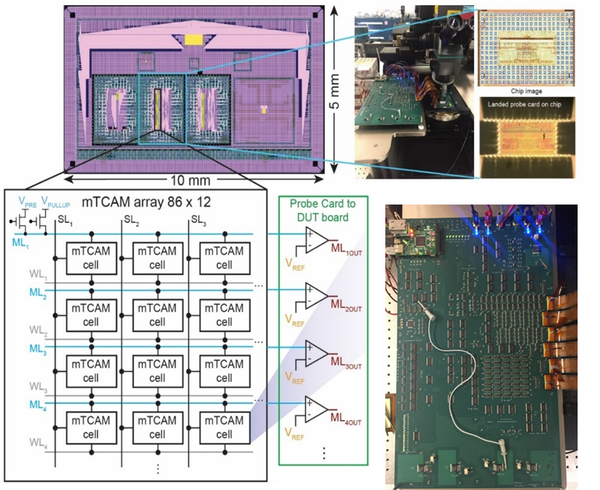
We have used these prototype chips, combined with larger system designs and simulations, to forecast significant speedups and lower power for security and genomics over state-of-the-art hardware available today.

We have taken steps to get closer to biological associative memories by leveraging the analog/continuous-valued properties of memristors in new CAM circuits. This has allowed the invention of an “analog CAM” with the ability to encode “fuzzy” ranges and even search with incomplete information. We see many opportunities for this core associative memory block in neuromorphic computing. And we have already found at least one “killer application” in the area of tree-based machine learning models (Decision Trees, Random Forests, etc). In this case, the root-to-leaf paths of the tree are directly mapped to the analog CAM array:

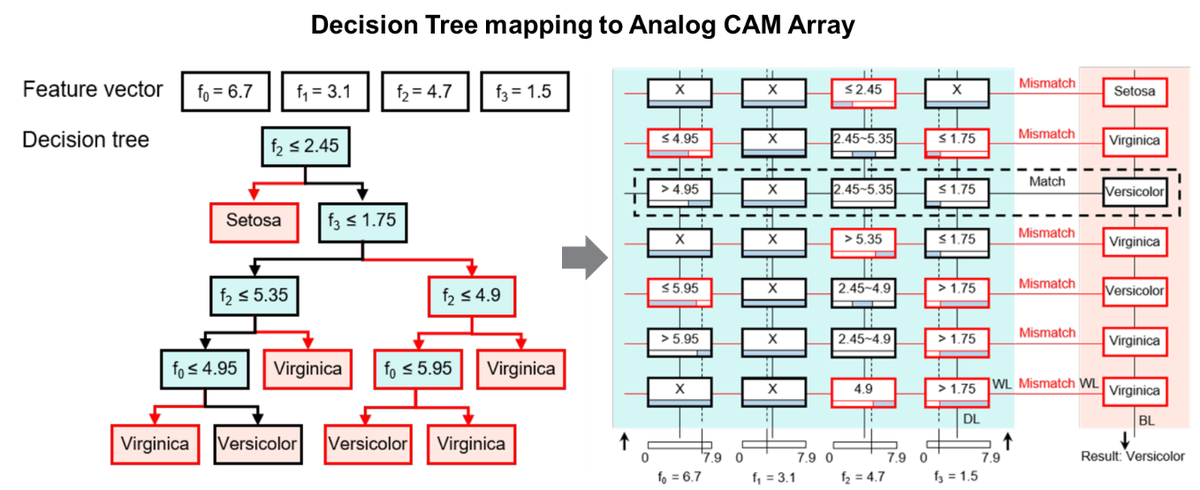
Our analysis shows that deploying many state-of-the-art tree models to a new analog CAM based architecture allows for blazingly fast inference at low energy (>100x faster and lower energy per decision). This is exciting because tree-based models are extremely popular by data scientists, require smaller data-sets to train, and rival deep learning networks in final accuracy. Another virtue is the resulting model offers increased interpretability and explainability over deep learning. We think this application area is just the tip of the ice-berg and are enthusiastically exploring other neuromorphic areas for the use of associative memory blocks.

Further reading:

• Analog content-addressable memories with memristors
• Tree-based machine learning performed in-memory with memristive analog CAM
• In-Memory Computing with Memristor Content Addressable Memories for Pattern Matching
• Memristor TCAMs Accelerate Regular Expression Matching for Network Intrusion Detection
• Regular Expression Matching with Memristor TCAMs for Network Security

In-memory computing for machine learning inference and training

A large domain of interest for non-von Neumann computing architectures is to support deep learning and other modern machine learning techniques. Artificial neural networks are inspired by neuro-anatomical observations, with data flowing between layers of neurons and computations distributed throughout. This data flow has practically no resemblance to the CPU layout that follows a von Neumann design and leads to tremendous inefficiency when a CPU tries to run the computations needed in neural networks. GPUs offer a great improvement here and are the gold standard today. But there is significant room for improvement, and future machine learning that adopts even more biological inspiration will only make this gap larger.

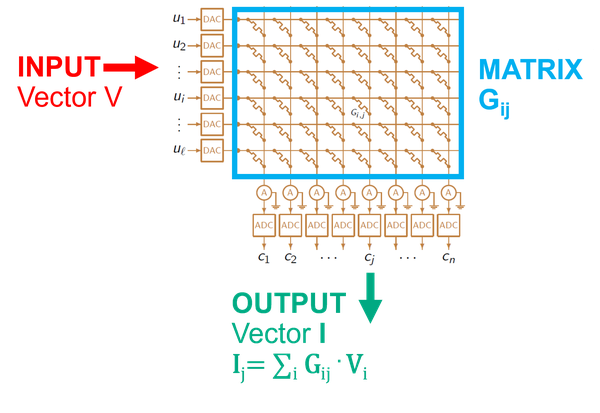
Our team and collaborators have spent many years exploring new architectures better matched to neural network inference and training. Some key insights are that brains operate through intertwined compute/memory operations, and furthermore that high precision calculations are not required, but are unnecessarily costly. The vast majority of computations performed in artificial neural networks are matrix operations (linear algebra). And the majority of energy and time expended for these computations comes from fetching and moving the required data (synaptic weights and activations) across a chip. Both of these are addressed with the use of non-volatile analog memristors that can store synaptic weight values and allow for performing matrix operations within the memory itself: in-memory computing. A circuit layout that allows this is a simple crossbar geometry. With weights stored in the memristor crossbar cells as conductance, when the input vector is applied to row lines, the matrix-vector multiplication out is generated as the current in the column lines.

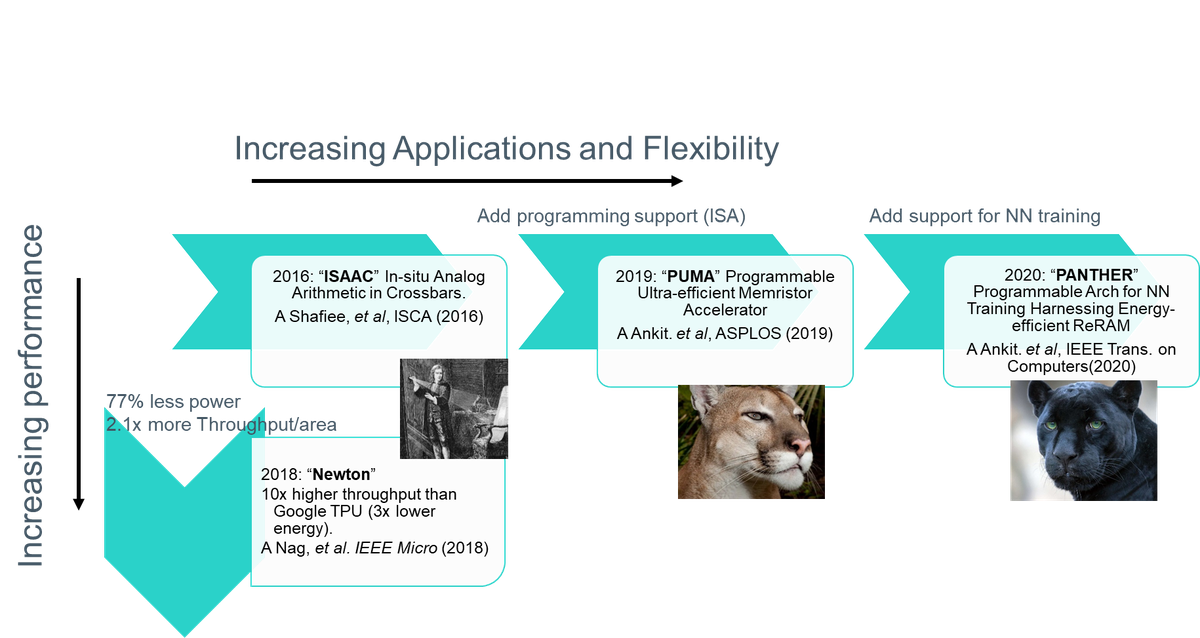
Using this basic circuit, and supplementing with many digital function blocks, larger architectural designs are constructed that can support any modern deep learning network, from Convolutional Neural Networks (CNN) to Long Short-Term Memory (LSTM) and Restricted Boltzmann Machines (RBM). Our work began with a design we called “ISAAC” (In-situ Analog Arithmetic in Crossbars), published in 2016 International Symposium on Computer Architecture (ISCA). The work has since evolved in different directions, either increasing performance with more optimizations, or increasing breadth by adding more flexible design and functionality to support more network types, and even support for the harder problem of neural network training (PANTHER).

Further reading:

• Memristor-Based Analog Computation and Neural Network Classification with a Dot Product Engine
• CMOS-integrated nanoscale memristive crossbars for CNN and optimization acceleration
• Low-Conductance and Multilevel CMOS-Integrated Nanoscale Oxide Memristors
• Analog error correcting codes for defect tolerant matrix multiplication in crossbars
• The future of electronics based on memristive systems
• Analogue signal and image processing with large memristor crossbars
• ISAAC: a convolutional neural network accelerator with in-situ analog arithmetic in crossbars
• Newton: Gravitating Towards the Physical Limits of Crossbar Acceleration
• PUMA: A Programmable Ultra-efficient Memristor-based Accelerator for Machine Learning Inference
• PANTHER: A Programmable Architecture for Neural Network Training Harnessing Energy-Efficient ReRAM

Research groups

Adaptive In-Memory Computing (AIM) Research Group led by Dr. Ming-Jay Yang