Mathematical Methods
Theoretical physics relies on advanced mathematical and physical theories, concepts and tools to study the dynamics of physical systems. Understanding formal mathematical structures is thereby crucial to better our understanding of the laws and principles of Nature.
Mathemtical Methods research is performed using analytical tools only (i.e., pen and paper), and computational resources are used only to graphically represent the insights gained. This line of research is particularly interested in obtaining formal expressions that encode physical aspects of interest as generally as possible, not in optimizing or simulating particular tasks or processes.
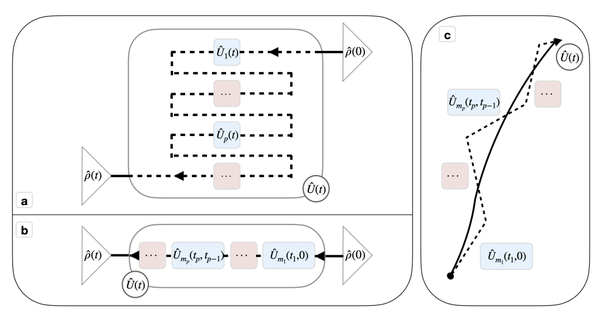
This avenue of research comprises many studies of the formal structures of mathematical physics, with particular attention to quantum physics, quantum information and quantum field theory in flat or curved spacetime.
Research group: Mathematical Physics
Research topics:
- Cavity quantum field dynamics
- Covariance Matrix Formalism
- Quantum Dynamics and Time Evolution
- Quantum Information
- Symplectic Geomentry and Lie Algebra
External Links:
- Continuous variable quantum information: Gaussian states and beyond review by G. Adesso, S. Ragy, A. R. Lee
