Spin-Related Transport
Spin torque by Spin-Hall effect
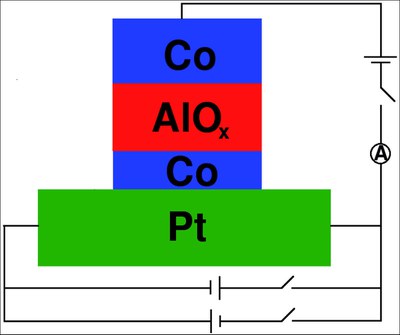
In the presence of a longitudinal electric field electrons in solids acquire spin-dependent transverse velocities, which are equal but opposite for spin-up and spin-down electrons in paramagnets, resulting in a pure spin current. This so-called spin Hall effect, which arises due to the spin-orbit interaction, is thought to play an important role in future generations of spintronic devices, because it allows to access the spin degree of freedom of the electron without making use of external magnetic fields. Transition metals, in particular the 4d and 5d ones, often exhibit a very large spin Hall effect. The transverse spin currents due to the spin Hall effect in transition metals are often so large that they allow to switch the magnetization in an adjacent thin ferromagnetic layer. This mechanism can be exploited in a 3 terminal realization of the MRAM, shown in the figure: The current direction in the Pt controls the sign of the spin current flowing into the thin cobalt layer. Thereby, the magnetization of the thin cobalt layer can be switched reversibly. A second circuit is used for reading the magnetic configuration via the tunnel magnetoresistance effect.
Anisotropy of Spin-Hall effect

While symmetry dictates spin-polarization and spin current to be mutually orthogonal and to be orthogonal to the driving electric field in cubic paramagnets, hexagonal paramagnets allow to tune the angle between spin polarization and spin velocity via the direction of the electric field, due to the anisotropy of the spin Hall effect in hexagonal metals. The anisotropies of the spin Hall effect in hexagonal transition metals are often large (see figure). If the spin Hall effect changes sign as a function of electric field direction (see e.g. Sc, Ti and Ru in the figure), one can even realize transverse spin currents with spin polarization parallel to the spin current. This results in a very large tunability -- which involves both magnitude of the effect and angle between polarization and spin current -- of the transverse spin current flowing in x-direction via the orientation of the driving electric field in the yz plane of the hexagonal crystal.
5d Adatoms on Graphene: the Making of a Chern Insulator
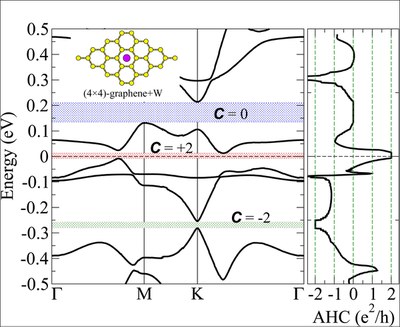
Quantum anomalous Hall effect in graphene decorated by W adatoms. We have done calculations of graphene in 4x4 supercell with 5d transition metals adatoms using the FLEUR code. The hybrid systems display remarkable physcial properties, e.g. significant magnetic moments on 5d adatoms, colossal magnetocrystalline anisotropy and strong magnetoelectric response. More interestingly, we observed that there exist topological nontrivial gaps in the hybrid systems, where the anomalous Hall conductivity (AHC) is quantized in units of e2/h. For instance, in (4x4)-graphene+W, there are several gaps opened due to spin-orbit coupling, the topological non-triviality of the gaps is clearly manifested by the AHC calculated (cf. figure).
For more details, please refer to Phys. Rev. Lett. 108, 056802 (2012).
Spin relaxation in metals

Shown is the Fermi surface of tungsten in the First Brillouin zone, with the spin-mixing parameter in a color-code. In the presence of spin-orbit coupling, the electronic states are not of pure but of mixed spin character. Points of full spin mixing (value of 0.5) are called 'spin hot spots' (red regions in the picture). The direction of the spin-quantization axis is illustrated by the red arrow. For the phenomenon of spin-relaxation in spin-transport processes, the spin-mixing parameter on the Fermi surface is of fundamental importance.
(Ph. Mavropoulos)
Spin injection from Fe into Si
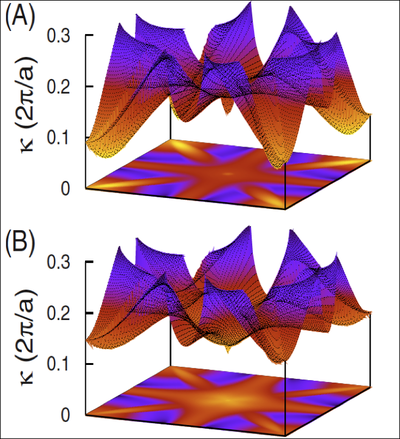
Spin injection from ferromagnets into Si is an important goal in spintronics, because it allows to retain Si technology. We studied the possibility of spin injection from Fe into Si(001) assuming a Si Schottky barrier at the interface. We used ab-initio calculations (KKR Green function method) and the Landauer approach to transport. We found that changing the position of the Fermi level in the Si barrier can significantly influence the injection efficiency due to state filtering in the Brillouin zone.
The figure shows the complex band structure (decay parameter) at EF in the band gap of Si in the 001 direction for EF=Ev +0.725 eV (A) and at EF=Ev+0.325 eV (B). Depending on the position of the Fermi energy in the gap, either the center or the corners of the Brillouin zone dominate the tunneling current.
For details see P. Mavropoulos, Phys. Rev. B 78, 054446 (2008).
(Ph. Mavropoulos)
