Energie Netzwerke und Komplexe Systeme
Über
Die Forschungsgruppe Energie Netzwerke und komplexe Systeme entwickelt mathematische Methoden und Werkzeuge für einen stabilen Betrieb der elektrischen Stromnetze. Ein Schwerpunkt unserer Arbeit ist die Stabilität und Robustheit gegenüber Ausfällen und Gerätefehlern. Wir verwenden Simulationen und Konzepte der mathematischen Graphentheorie, um zu verstehen, was ein Stromnetz anfällig macht und wie wir stabile und robuste Netze entwerfen können. Ein zweiter Schwerpunkt ist die Steuerung des Stromnetzes und die Interaktion mit anderen Teilen des Energiesystems. Mithilfe von Methoden des maschinellen Lernens quantifizieren und erklären wir, wie sich äußere Einflüsse und Störungen auf den Betrieb des Stromnetzes auswirken.
Forschungsthemen
Algebraische Graphentheorie und ihre Anwendungen
Erklärbares und kausales maschinelles Lernen für Energiesystemanwendungen
Last-/Frequenzsteuerung
Robustheit von Übertragungsnetzen und kaskadierende Ausfälle
Optimierung von Netztopologien
Members
FORSCHUNGSFELDER
Algebraische Graphentheorie und ihre Anwendungen
Wir verwenden Konzepte der algebraischen Graphentheorie, um die Robustheit von Energienetzen zu analysieren und Algorithmen für die Analyse und den Betrieb von Energiesystemen zu entwickeln. Die Abbildung unten zeigt, dass gängige Optimierungsprobleme in der Stromnetzplanung durch Umformulierung der zugrundeliegenden Netzgleichungen wesentlich schneller gelöst werden können.
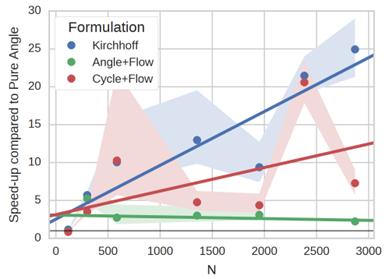
(Für weitere Details siehe https://doi.org/10.1016/j.epsr.2017.12.034)
Erklärbares und kausales maschinelles Lernen für Energiesystemanwendungen
Die Energiewende führt zu einer enormen Zunahme von Komplexität und Unsicherheit. Gleichzeitig werden große Datenmengen verfügbar, die neue Einblicke in den Betrieb von Energie- und Leistungssystemen ermöglichen. Wir wenden Werkzeuge aus der (kausalen) Statistik und dem maschinellen Lernen an, um unser Verständnis der komplexen Wechselwirkungen verschiedener Systeme und Märkte zu verbessern.
Die folgende Abbildung zeigt Gemeinschaften von Strommärkten vor und während der europäischen Stromkrise. Die Gemeinschaften stark integrierter Märkte in Nord- und Osteuropa wurden zerrüttet, da sie unterschiedlich auf die Krise reagierten.
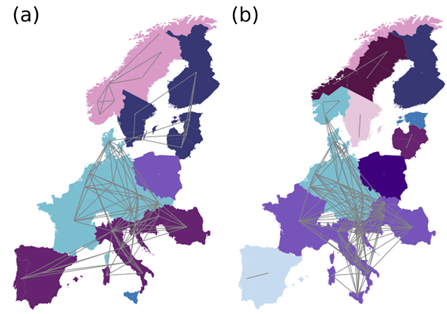
(Für weitere Details siehe https://doi.org/10.1063/5.0201734)
Last-Frequenz-Steuerung
TDie Netzfrequenz ist eine der zentralen Messgrößen bei der Steuerung von Stromnetzen, da sie das Gleichgewicht von Erzeugung und Last misst. Sie wird verwendet, um den Betrieb von Reservekraftwerken zu steuern, die das Gleichgewicht im Netz in Echtzeit wiederherstellen. Wir entwickeln transparente Methoden des maschinellen Lernens, um Bedrohungen der Frequenzstabilität zu erkennen und den Regelungsbedarf vorherzusagen. Die Abbildung unten zeigt die Architektur eines physikalisch informierten ML-Modells für die probabilistische Vorhersage von Frequenzverläufen.
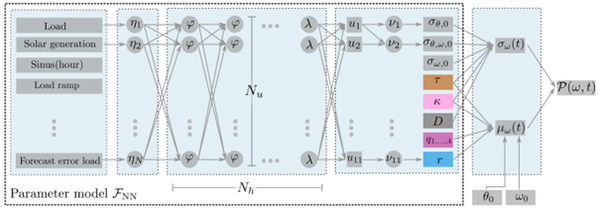
(Abbildung entnommen aus https://doi.org/10.1103/PRXEnergy.2.043003)
Robustheit von Übertragungsnetzen und Kaskadenausfälle
Kaskadenausfälle gehören zu den größten Bedrohungen für die Stabilität der Stromnetze. Der Ausfall eines einzelnen Übertragungsnetzes kann einen Dominoeffekt auslösen, der zu weiteren Ausfällen und schließlich zu einer Fragmentierung des Netzes führt. Wir analysieren das Risiko solcher Kaskadenausfälle sowohl mit analytischen Methoden als auch mit groß angelegten Simulationen. Die Abbildung unten zeigt, wie eine modifizierte Netztopologie die Ausbreitung von Ausfällen und damit großflächige Kaskaden unterdrücken kann.
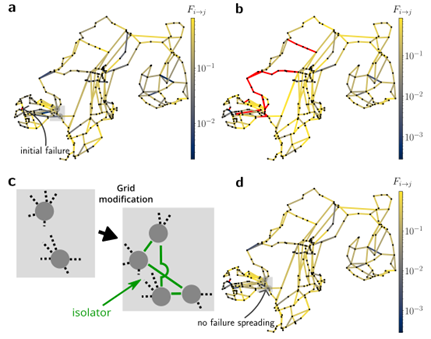
(Abbildung entnommen aus https://doi.org/10.1038/s41467-021-23292-9)
Optimierung von Netztopologien
Die Energiewende führt zu steigenden Belastungen in den Hochspannungsnetzen. Die Übertragungsnetzbetreiber müssen häufig eingreifen, um Engpässe abzubauen und das Netz stabil zu halten. Diese Maßnahmen verursachen Kosten in Milliardenhöhe und führen zu zusätzlichen Treibhausgasemissionen. Die dynamische Rekonfiguration der Topologie ist eine vielversprechende Maßnahme zur Bewältigung von Engpässen in der bestehenden Infrastruktur. Die Topologieoptimierung ist mathematisch anspruchsvoll, so dass neuartige Algorithmen erforderlich sind, um diese Option zu realisieren.

