Precision Spectroscopy of the Hydrogen Hyperfine Structure
Precision spectroscopy is nowadays performed with tunable lasers, which are sent to cold atoms at rest to induce transitions. In combination with a frequency comb, a relative energy resolution of up to 10-13 and in absolute values of 10-12 eV has been achieved for the 2S-1S transition in hydrogen.
Using the components of a Lamb-shift polarimeter and a magnetic field oscillating along the beam axis, it is now possible to observe motion-induced or “resonant coherent excitation” transitions between the hyperfine structure sub-states of hydrogen with an energy difference of a few neV. In this case, a beam of metastable atoms in a single hyperfine state passed through a static magnetic field generated by two opposing solenoids. The longitudinal field component has a nearly sinusoidal shape, so that the passing atom experiences a temporally oscillating magnetic field in its rest frame. The effective value of the maximum fields in the center of the coils defines the average magnetic field experienced by the atom, which corresponds to the x-axis in the Breit-Rabi diagram (see Fig. 2).
The time of flight Δt depends on the velocity of the beam v and the distance between the coils, which corresponds approximately to a (wave-) length λ. The frequency of this oscillation is therefore
f = 1/Δt = v/λ
and the energy of the corresponding virtual photons following the Planck-Einstein relation is
EPh = h ∙ f = h ∙ v/λ .
Here it should be mentioned that only a radial field oscillations induces magnetic dipole transitions with ΔmF = ± 1, but due to the Maxwell equations the radial field Brad. is determined as
Brad. (z,r) = - dBlong /dz ∙ r/2 .
Thus, the wavelength λ stays constant in first order.
During the experiments at IKP the beam energy is in the order of 1 keV, i.e. the velocity of the incoming atoms is in the range of v ≈ 105 m/s. With a wavelength ofλ ~ 0.1 m, the corresponding frequency is 1 MHz and the energy of this coherent photon pulse is EPh ~ 1 neV. The beam velocity and the wavelength are measured with a relative uncertainty of 10-3, so that the total uncertainty can be 10-12 eV, a similar value to the most precise measurements above. Furthermore, all odd multiples of this energy will also induce transitions if the sum of the photon energies corresponds to the energy difference between the hyperfine states at a corresponding magnetic field in the Breit-Rabi diagram.
The photon energy itself can be manipulated either by changing the distance between the coils (λ) or by changing the beam energy (v). In this way, the energy of this coherent photon pulse is tunable in a large range and, therefore, a large number of various measurements is possible. The wavelength can be chosen between 10-10 m (Distance of nucleons in a crystal) and 1 m and the velocity can be handled between 102 (thermic beams) and 108 m/s (accelerator based). Thus, the photon energy ranges from keV down to peV. Instead of a single pulse, even many repetitions of the oscillations are possible and depending of electric or magnetic field oscillations even electric or magnetic dipole transitions can be induced. Further improvements are of course possible …
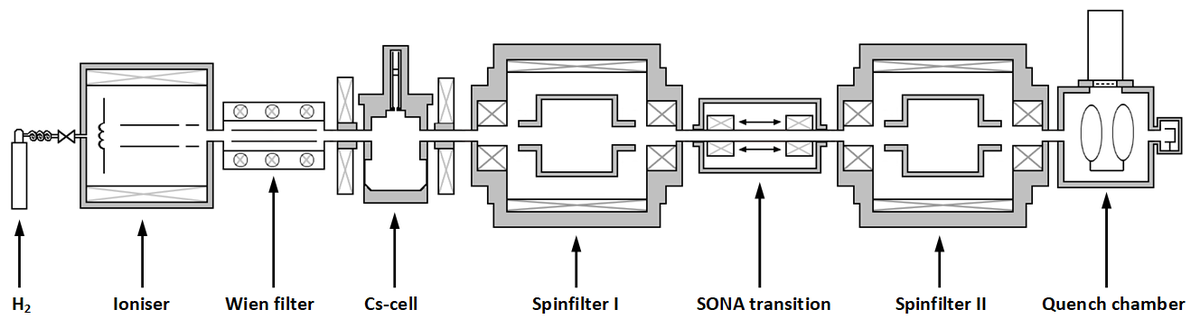
As shown in the figure above, the experimental setup starts with an ECR source that generates an intense proton beam with a sharp energy in the range of a few keV. Next, a Wien filter is used to separate the protons from all other ions produced by the source and even helps to determine the beam velocity more accurately. Charge exchange with cesium vapor produces metastable hydrogen atoms in all four hyperfine structure sub-states. Subsequently, the spin filter of a Lamb-shift polarimeter separates a single hyperfine state, either α1 (mJ=+1/2, mI=+1/2) or α2 (mJ=+1/2, mI=-1/2). The oscillating static field of the two solenoids has two effects on the population numbers: First, it induces an exchange of the occupation numbers of the α1 and β3 sub-states (mJ=-1/2, mI=-1/2) by non-adiabatically rotating the direction of the external magnetic field by 180°. In parallel, the magnetic field oscillation can be interpreted as a “single radio wave laser pulse”, since all photons are coherent, i.e. oscillate in phase. Thus, transitions between the hyperfine states β3 ↔ α2 and α2 ↔ α1 are induced by absorption and stimulated emission as long as the energy difference between these states corresponds to an odd multiple of the fundamental energy EPh = h ∙ v/λ and the respective states are occupied or not. A second spin filter then transmits only metastable atoms in the α1 or α2 state, the number of which can be measured. For this purpose, the remaining metastable atoms are quenched to the ground state by a strong electric field (Stark effect) and the Lyman-α photons generated in this way are measured with a photomultiplier. The number of photons generated corresponds to the occupation number of the respective substates. The results can be seen in the following figure.

This new method enables controlled direct transitions between quantum states in an energy range below 10 neV. This should make it possible to test the expected QED corrections of the binding energies in the order of 10-12 eV. The figure above shows deformations of the peaks caused by the interference of the transitions between the three states. The spin filters can also be modified so that both α-states pass simultaneously. This allows a transition of atoms in the β3 state into a superposition of both α states to be observed. Another possible extension of this experiment is a new type of spin filter that is currently being developed. This modified spin filter will make it possible to measure the occupation numbers of both β-states separately, which will make the measurements overdetermined.
Of course, the measured spectra can also be simulated using the density matrix formalism based on the known Hamiltonian of the hyperfine interaction and the measured magnetic field distribution B(z) that are implemented to solve the von Neumann equation.
