Präzisionsspektroskopie der Hyperfeinstruktur des Wasserstoffs

Präzisionsspektroskopie wird heutzutage mit abstimmbaren Lasern durchgeführt, die auf kalte, ruhende Atome geschickt werden, um Übergänge zu induzieren. In Kombination mit einem Frequenzkamm wurde für den 2S-1S-Übergang im Wasserstoff eine relative Energieauflösung von bis zu 10^-13 und in absoluten Werten von 10^-12 eV erreicht.

Mit den Komponenten eines Lambshift Polarimeters und einem Magnetfeld, das entlang der Strahlachse oszilliert, ist es nun möglich, Übergänge zwischen den Hyperfeinstruktur-Unterzuständen des Wasserstoffs mit einer Energiedifferenz von wenigen neV zu beobachten. In diesem Fall wird ein Strahl metastabiler Atome in einem einzelnen Hyperfeinzustand durch ein statisches Magnetfeld zweier Solenoide mit entgegengesetzter Richtung geschickt. Die longitudinale Feldkomponente hat eine nahezu sinusförmige Form, so dass das durchlaufende Atom in seinem Ruhezustand ein zeitlich oszillierendes Magnetfeld erfährt. Der Effektivwert der maximalen Felder in der Mitte der Spulen definiert das durchschnittliche Magnetfeld, welches das Atom erfährt und das der x-Achse im Breit-Rabi-Diagramm (siehe Abb. 2) entspricht. Die Flugzeit Δt hängt von der Geschwindigkeit des Strahls v und dem Abstand der Spulen ab, der ungefähr einer (Wellen-) Länge λ entspricht. Die Frequenz ist also

f =1/Δt = v/λ

und die Energie der entsprechenden virtuellen Photonen folgt der Planck-Einstein-Beziehung

E_Ph = h · f = h · v/λ .

Hier sollte erwähnt werden, dass nur eine radiale Feldschwingung magnetische Dipolübergänge mit Δm_F = ± 1 induziert, aber aufgrund der Maxwell-Gleichungen ist das radiale Feld B_rad. bestimmt als

B_rad. (z,r) = - dB_long /dz ∙ r/2.

Somit bleibt die Wellenlänge λ in erster Ordnung konstant.

Während der Experimente am IKP liegt die Strahlenergie in der Größenordnung von 1 keV, d.h. die Geschwindigkeit der einfallenden Atome liegt im Bereich von v ≈ 10⁵ m/s. Bei einer Wellenlänge von λ ~ 0,1 m liegt die entsprechende Frequenz bei 1 MHz und die Energie dieses kohärenten Photonenpulses bei E_Ph~ 1 neV. Die Strahlgeschwindigkeit und die Wellenlänge werden mit einer relativen Unsicherheit von 10^-3 gemessen, so dass die Gesamtunsicherheit 10^-12 eV betragen kann, ein ähnlicher Wert wie bei den genauesten Messungen oben. Außerdem werden alle ungeraden Vielfachen dieser Energie ebenfalls Übergänge induzieren, wenn die Summe der Photonenenergien der Energiedifferenz zwischen den Hyperfeinzuständen bei einem entsprechenden Magnetfeld im Breit-Rabi-Diagramm entspricht.

Die Photonenenergie selbst kann entweder durch Änderung des Abstands zwischen den Spulen (λ) oder durch Änderung der Strahlenergie (v) manipuliert werden. Auf diese Weise ist die Energie dieses kohärenten Photonenpulses in einem großen Bereich abstimmbar, so dass eine große Anzahl verschiedener Messungen möglich ist. Die Wellenlänge kann zwischen

10^-10 m (Abstand der Nukleonen in einem Kristall) und 1 m gewählt werden, und die Geschwindigkeit kann zwischen 10² (thermische Strahlen) und 10⁸ m/s (beschleunigerbasiert) gehandhabt werden. Die Photonenenergie reicht also von keV bis hinunter zu peV. Anstelle eines einzelnen Pulses sind auch viele Wiederholungen der Schwingungen möglich und in Abhängigkeit von elektrischen oder magnetischen Feldschwingungen können sogar elektrische oder magnetische Dipolübergänge induziert werden. Weitere Verbesserungen sind natürlich möglich ...

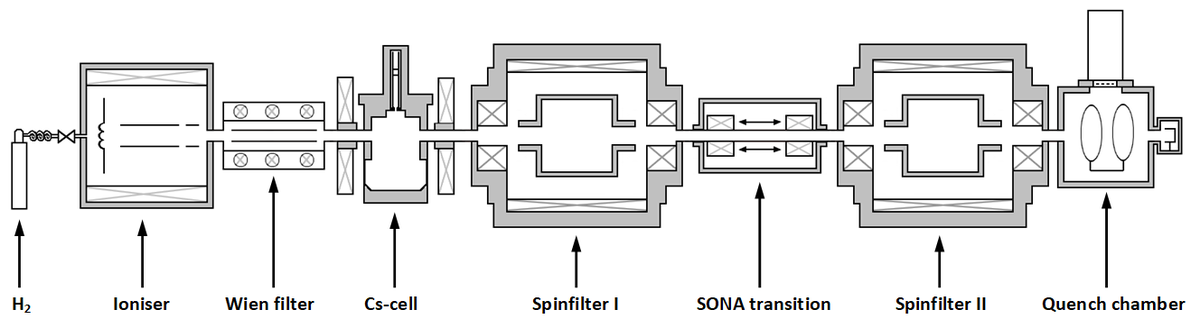
Wie in der Abbildung oben dargestellt, beginnt der Versuchsaufbau mit einer ECR-Quelle, die einen intensiven Protonenstrahl mit einer scharfen Energie im Bereich von wenigen keV erzeugt. Als Nächstes wird ein Wien-Filter verwendet, der die Protonen von allen anderen von der Quelle erzeugten Ionen trennt und der sogar hilft die Strahlgeschwindigkeit genauer zu bestimmen. Durch Ladungsaustausch mit Cäsiumdampf werden metastabile Wasserstoffatome in allen vier Hyperfeinstruktur-Unterzuständen erzeugt. Anschließend separiert der Spinfilter eines Lambshift Polarimeters einen einzelnen Hyperfeinzustand, entweder α1 (m_J=+1/2, m_I=+1/2) oder α2 (m_J=+1/2, m_I=-1/2). Das oszillierende statische Feld der Sona-Übergangseinheit hat zwei Auswirkungen auf die Besetzungszahlen: Erstens induziert es einen Austausch der Besetzungszahlen der Unterzustände α1 und β3 (m_J=-1/2, m_I=-1/2), indem es die Richtung des externen Magnetfelds nichtadiabatisch um 180° dreht. Parallel dazu kann die Magnetfeldoszillation als ein "Radiowellen-Laserimpuls" interpretiert werden, da alle Photonen kohärent sind, d.h. in Phase schwingen. So werden durch Absorption und induzierte Emission Übergänge zwischen den Hyperfeinzuständen β3 ↔ α2 und α2 ↔ α1 induziert, solange die Energiedifferenz zwischen diesen Zuständen einem ungeraden ganzzahligen Vielfachen der Grundenergie E = h · v/λ entspricht und die jeweiligen Zustände besetzt sind oder nicht. Ein zweiter Spinfilter transmittiert anschließend ausschließlich metastabile Atome im Zustand α1 oder α2, deren Anzahl gemessen werden kann. Dazu werden die verbleibenden metastabilen Atome durch ein starkes elektrisches Feld in den Grundzustand gequencht werden (Stark-Effekt) und die so erzeugten Lyman-α-Photonen mit einem Photomultiplier gemessen. Die Anzahl der dabei erzeugten Photonen entspricht der Besetzungszahl der jeweiligen Unterzustände. Die Ergebnisse sind in der folgenden Abbildung zu sehen.

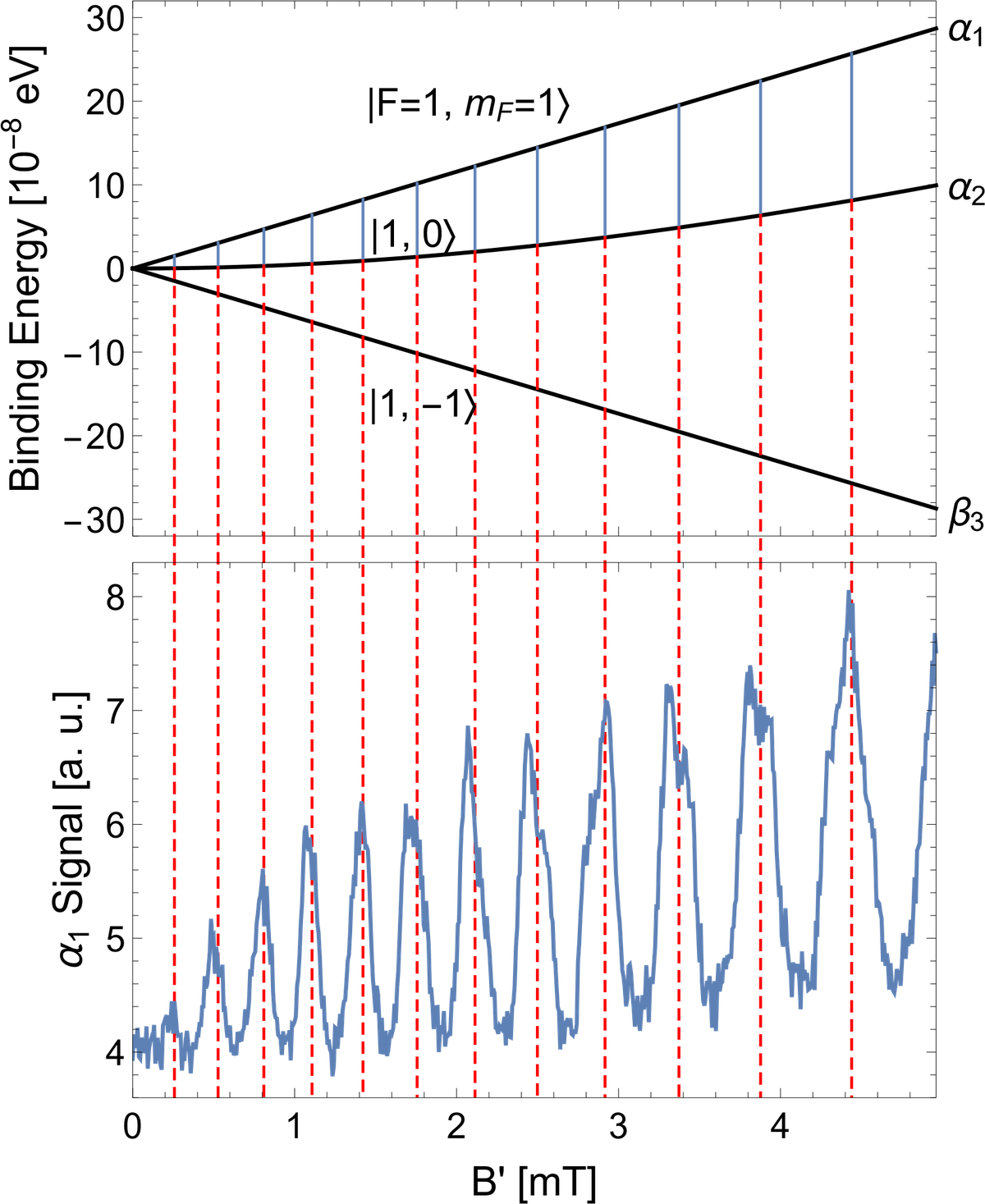
Diese neue Methode erlaubt es, Übergänge zwischen Quantenzuständen in einem Energiebereich unter 10 neV direkt zu induzieren. Damit sollte es möglich sein, die erwarteten QED-Korrekturen der Bindungsenergien in der Größenordnung 10^-12 eV zu testen. In der obigen Abbildung sind Verformungen der Peaks zu erkennen, die durch die Interferenz der Übergänge zwischen den drei Zuständen hervorgerufen werden. Die Spinfilter können jedoch so modifiziert werden, dass sie beide α-Zustände gleichzeitig durchlassen. Dadurch kann ein Übergang von Atomen im β3-Zustand in eine Superposition beider α-Zustände beobachtet werden. Eine weitere mögliche Erweiterung dieses Experiments wäre ein neuer Typ von Spinfilter, der derzeit entwickelt wird. Dieser modifizierte Spinfilter wird es ermöglichen, die Besetzungszahlen beider β-Zustände getrennt zu messen, wodurch die Messungen überbestimmt sein werden.

Natürlich können die gemessenen Spektren auch mit Hilfe des Dichtematrix-Formalismus simuliert werden, der auf dem bekannten Hamiltonian der Hyperfein-Wechselwirkung und der gemessenen Magnetfeldverteilung B(z, r) basiert, die zur Lösung der von-Neumann-Gleichung eingesetzt werden.