Transport processes in porous materials

The electrochemical conversion in fuel cells and electrolysers takes place on small spatial scales in the nanometer range. From a process engineering perspective, these are functional layers that have certain homogeneous transport properties from a macroscopic point of view. The functional layers are porous transport layers with structures in the micro- and nanometer range. Porous materials consist of irregularly arranged structures. Transport simulations show strong local scattering of velocities and flows caused by the local arrangement of geometric objects. If the material is compressed, not only the homogenized material properties change, but also the scattering range of the local velocities.

Stochastic aspects

The microstructures of porous layers show large local differences. Therefore, stochastic geometry models are used in addition to real structures, for example from nano-CT images, to create three-dimensional geometries that are stochastically equivalent to the real microstructure. The figure shows two exemplary realizations of a geometry model that are stochastically equivalent to the real structure of a gas diffusion layer (GDL). They consist of 26 fiber layers, here with a spatial resolution of 5 image points per fiber diameter. For the visualization, the two upper fiber layers were colored. This highlights local differences in the fiber placement.

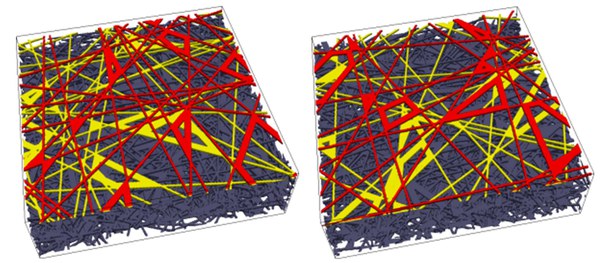
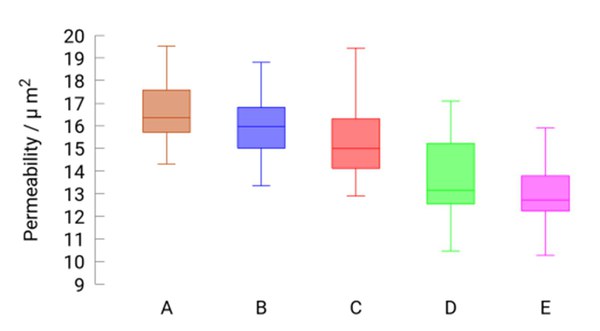
The transport of gases and two-phase mixtures is simulated using the Lattice-Boltzmann method on the JSC supercomputer JURECA. Both in-house and open source tools are used for this purpose. Up to 1600 computer cores are currently used for the simulation on 30 to 500 million cells. Nevertheless, it is doubtful that simulations on a single Dömane are representative in terms of local physical processes - after all, the image section shown above represents less than 1 mm² of the material. The stochastic component of the geometry model emulates situations at different positions of the material, similar to how real three-dimensional images of the microstructure would show differences in the details at different positions. Statistical scatter in input data - stochastic geometries are nothing else - leads to statistical scatter in the calculation results, i.e. also in extensive simulations. This is exemplified by the scattering of permeabilities. 25 representations of the geometry model were combined with five variants in which the binder can be arranged between the fibers (A to E in the image). The permeability was determined from 125 transport simulations. The scatter for each group (A to E) is represented by a box plot showing the minimum and maximum as well as the 25%, 50% and 75% quantiles.

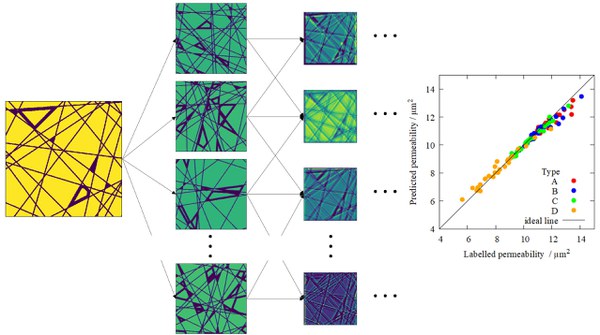
Predicting the permeability of porous transport layers using neural networks

In the work presented here, the prediction of permeability in fiber-based gas diffusion layers by neural networks is presented. Based on a set of geometric microstructures and the corresponding permeabilities calculated by Lattice-Boltzmann simulations, a neural network was developed and trained to predict the permeability of such paper-like structures. Starting from a base model, the network architecture and hyperparameters were systematically optimized. These optimizations led to a reduction of the mean square error of the predictions by 68 % compared to the data set used for the tests. The final model is able to predict permeabilities of microstructures with a relative deviation of 5.29%, which is well below the underlying variance of the stochastic model used to generate the data used. The accuracy of the optimized model was further validated using five-fold cross-validation, which confirmed the results. The training of the neural network requires significant computational resources, preferably GPUs; however, the prediction of permeability can be performed on conventional desktop computers. The neural network operates on the three-dimensional microstructures; a two-dimensional plane was chosen for visualization.

Further potential applications of machine learning methods lie in the efficient prediction of the dynamic behavior of electrochemical systems.

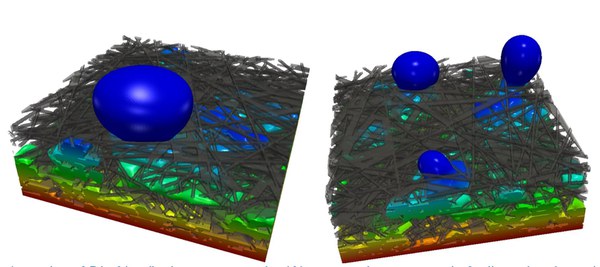
Two-phase simulations

Gas diffusion layers (GDL) consist of carbon fibers that are naturally hydrophilic. The coating with polytetrafluoroethylene (PTFE) creates a desired hydrophobic property of the coated fibers. In addition to the stochastic characteristics of the fiber layers, a statistical distribution of PTFE is created along the fibers - generally only the total amount of PTFE used is really known. Due to the statistical characteristics of the microstructure, water droplets that emerge from the GDL on the cathode side of a fuel cell are not only found in randomly distributed locations, but also have asymmetrical droplet shapes - also due to the irregular fiber structure - which form different contact angles with the rough GDL surface depending on the viewing plane.

Literature:

D. Froning, U. Reimer, W. Lehnert. Inhomogeneous Distribution of Polytetrafluorethylene
in Gas Diffusion Layers of Polymer Electrolyte Fuel Cells, Transp. Porous Media 163 (2021) 843-862, https://doi.org/10.1007/s11242-021-01542-0

D. Froning, M. Drakselová, A. Tocháčková, R. Kodým, U. Reimer, W. Lehnert, K. Bouzek, Anisotropic properties of gas transport in non-woven gas diffusion layers of polymer electrolyte fuel cells. Journal of Power Sources 425, 227828 (2020), https://doi.org/10.1016/j.jpowsour.2020.227828

J. Yu, D. Froning, U. Reimer, W. Lehnert
Polytetrafluorethylene effects on liquid water flowing through the gas diffusion layer of polymer electrolyte membrane fuel cells. J. Power Sources 438 (2019) 226975 https://doi.org/10.1016/j.jpowsour.2019.226975

J. Yu, D. Froning, U. Reimer, W. Lehnert
Apparent contact angles of liquid water droplet breaking through a gas diffusion layer of polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 43 (2018) 6318-6330 https://doi.org/10.1016/j.ijhydene.2018.01.168

D. Froning, J. Yu, U. Reimer, W. Lehnert
Stochastic Analysis of the Gas Flow at the Gas Diffusion Layer/ Channel Interface of a High-Temperature Polymer Electrolyte Fuel Cell. Appl. Sci. 8 (2018), 2536 https://doi.org/10.3390/app8122536

D. Froning, J. Yu, G. Gaiselmann, U. Reimer, I. Manke, V. Schmidt, W. Lehnert
Impact of compression on gas transport in non-woven gas diffusion layers of high temperature polymer electrolyte fuel cells. J. Power Sources 318 (2016) 26-34 https://doi.org/10.1016/j.jpowsour.2016.03.102

D. Froning, J. Yu, U. Reimer, W. Lehnert
Statistische Analyse des lokalen Wassertransportes einer Polymer-Elektrolyt-Brennstoffzelle. Chem. Ing. Tech. 91 (2019) 865-871 https://doi.org/10.1002/cite.201800158

J. Yu, D. Froning, U. Reimer, W. Lehnert
Liquid water breakthrough location distances on a gas diffusion layer of polymer electrolyte membrane fuel cells. J. Power Sources 389 (2018) 56-60 https://doi.org/10.1016/j.jpowsour.2018.04.004

D. Froning, J. Brinkmann, U. Reimer, V. Schmidt, W. Lehnert, D. Stolten. 3D analysis, modeling and simulation of transport processes in compressed fibrous microstructures, using the Lattice Boltzmann method, Electrochimica Acta 110 (2013) 325-334. http://dx.doi.org/10.1016/j.electacta.2013.04.071

J. Wirtz, Untersuchung von neuronalen Architekturen für ein prediktives Modell der Eigenschaften von faserbasierten Gasdiffusionsschichten, Bachelor thesis, University of Applied Sciences, Aachen, 2021.

D. Froning, J. Wirtz, E. Hoppe, W. Lehnert. Flow characteristics of fibrous gas diffusion layers using machine learning methods, ACS Applied Materials & Interfaces, submitted.

W. Zou, D. Froning, X. J. Lu, W. Lehnert, An online spatiotemporal temperature model for high temperature polymer electrolyte fuel cells. Energy Conversion and Management 199 (2019) 111974, https://doi.org/10.1016/j.enconman.2019.111974

W. Zou, D. Froning, Y. Shi, W. Lehnert, A least-squares support vector machine method for modeling transient voltage in polymer electrolyte fuel cells. Applied Energy 271, 115092 (220), https://doi.org/10.1016/j.apenergy.2020.115092

W. Zou, D. Froning, Y. Shi, W. Lehnert, Working zone for a least-squares support vector machine for modeling polymer electrolyte fuel cell voltage, Applied Energy 283, 116191 (2021), https://doi.org/10.1016/j.apenergy.2020.116191

W. Zou, D. Froning, Y. Shi, W. Lehnert, An online adaptive model for the nonlinear dynamics of fuel cell voltage. Applied Energy 288, 116561 (2021), https://doi.org/10.1016/j.apenergy.2021.116561