Neural Networks: Chaos Pays Off
Jülich, 30 June 2021 – Creative geniuses have known it all along: Chaos improves your intellectual capacity. At least, it may be useful when it comes to networked neurons, as a scientific paper of Forschungszentrum Jülich has now shown. The newly discovered mechanism could also help speed up artificial neural networks used in artificial intelligence and machine learning applications.
Christian Keup from Prof. Moritz Helias’s research group “Theory of multi-scale neuronal networks” at INM-6 speaks about the results that have now been published in the journal Physical Review X.
Mr Keup, what new insights did your research group gain?
We were able to show that reliable information processing and chaos are not mutually exclusive. In some cases, they even benefit each other. This result is surprising since chaotic systems are normally considered unreliable. One example is the weather, which is very difficult to predict for more than two weeks but feasible over a few days, showing that the unreliability only occurs in the long term.
In neural networks, chaos even proves useful in the short term, amplifying any small change in the initial state of the network. Therefore, when providing sensory inputs to the network, any differences between them are also amplified. Our results show that strongly chaotic neural networks are better suited than less chaotic networks when arranging patterns into classes, for example. This is astonishing because chaos massively amplifies not only informative changes but also unimportant changes.

How are the results relevant for research and practice?
We have long known that biological neurons communicate through short electric impulses. In contrast, artificial neurons used in computer applications – such as for machine learning – send continuous signals.
Our results show that pulsed biological communication causes chaos in a different way, leading to very short processing times, which can also be observed in biological networks. A number of theoretical predictions can now be tested in neuroscientific experiments, and the theory invites researchers to use chaotic dynamics in machine learning and neuromorphic computing. These types of cross connections between neuroscience and artificial intelligence are often very useful – you just need to find an appropriate general mathematical formulation to see them.
Is there an explanation for why chaotic networks can process information so quickly?
A chaotic network causes all activity trajectories, i.e. signal trajectories that happen to be close to each other, to quickly move away from each other. The greater distance then facilitates ordering and grouping, for example when it comes to recognizing faces or categorizing the smell of a wine. Obviously, unimportant differences are also amplified. However, our calculations show that in networks with lots of neurons, these differences are outweighed by the beneficial effect in the short-term phase.
You can perhaps think of it as being similar to an unsolved Rubik’s Cube. Usually, you have to twist the cube many times to separate the different colours. However, in higher dimensions you could – to use a simple analogy – pull apart the individual stones, which represents the chaotic dynamics, and then put in a hyperplane, i.e. a kind of high-dimensional curtain, between the different colours, thus separating them from each other quite easily.
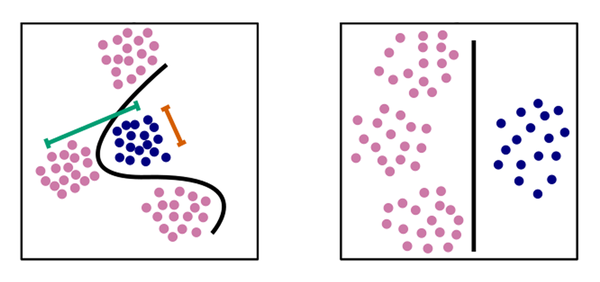
We – that is Moritz Helias, Tobias Kühn, David Dahmen, and I – have also calculated the optimal time for reading out the information, since the improvement in separability is only temporary. If you wait too long, the dynamics will start to mix everything up – chaotic systems are known for this kind of entropy production. However, “chaotic” does not mean “unpredictable” in this context. The state of the neural network largely evolves in a deterministic manner. In the long term, however, the strong sensitivity to disturbances means that this predictability is practically non-existent.
What method did you use to obtain the results?
We use statistical field theory to describe the probability distribution of the networks’ activity trajectories. This is a mathematical technique from theoretical physics. To understand the chaotic dynamics, i.e. how trajectories move away from each other, we performed a replica calculation: The trick is to copy the network so that you can track two trajectories at the same time. This allows us to calculate how the distance between the trajectories evolves.
Original publication:
Christian Keup, Tobias Kühn, David Dahmen, Moritz Helias
Transient Chaotic Dimensionality Expansion by Recurrent Networks
Physical Review X (25 June 2021), DOI: 10.1103/PhysRevX.11.021064
Further information:
Institute of Neuroscience and Medicine, Computational and Systems Neuroscience (INM-6 / IAS-6)
Contact:
Prof. Dr. Moritz Helias
Institute of Neuroscience and Medicine, Computational and Systems Neuroscience (INM-6 / IAS-6)
Tel: +49 2461 61-9647
Email: m.helias@fz-juelich.de
Christian Keup
Institute of Neuroscience and Medicine, Computational and Systems Neuroscience (INM-6 / IAS-6)
Tel: +49 2461 61-7620
Email: c.keup@fz-juelich.de
Press contact:
Tobias Schlößer
Press officer, Forschungszentrum Jülich
Tel: +49 2461 61-4771
Email: t.schloesser@fz-juelich.de
