Fehlertolerante und adaptive Zeitintegratoren

Viele PinT-Methoden weisen Merkmale auf, die sie zu natürlichen Kandidaten für algorithmenbasierte Fehlertoleranz (ABFT) machen: Sie halten Kopien der (Näherungs-)Lösung zu verschiedenen Zeiten auf verschiedenen Prozessoren und sind von Natur aus iterativ und/oder hierarchisch. Da der Zeitschritt typischerweise die äußerste Schleife für die numerische Lösung einer zeitabhängigen partiellen Differentialgleichung ist, deckt sein Schutz durch ABFT einen größeren Bereich des Codes ab. Bemühungen zur Bereitstellung von ABFT, z. B. auf der Grundlage von Zeitadaptivität, können gleichzeitig die Ausfallsicherheit und die Recheneffizienz erhöhen und sind sehr vielversprechend.

Fehlertolerant PFASST

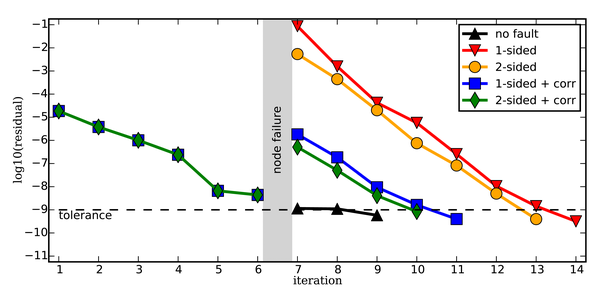
Wir führen verschiedene Strategien für das Parallel-in-Time-Integrationsverfahren PFASST ein und analysieren sie, um sich von harten Fehlern und nachfolgendem Datenverlust zu erholen. Da PFASST Lösungen in mehreren Zeitschritten auf verschiedenen Prozessoren speichert, können Informationen aus benachbarten Schritten zur Wiederherstellung verwendet werden, nachdem ein Prozessor ausgefallen ist. Die mehrstufige Hierarchie von PFASST ermöglicht es, die grobe Ebene für die Korrektur der rekonstruierten Lösung zu verwenden, was dazu beitragen kann, den Overhead zu minimieren.
_{Ref: Robert Speck, Daniel Ruprecht , Toward fault-tolerant parallel-in-time integration with PFASST, Parallel Computing, Vol.62, 20-37, 2017.}

Adaptiv SDC

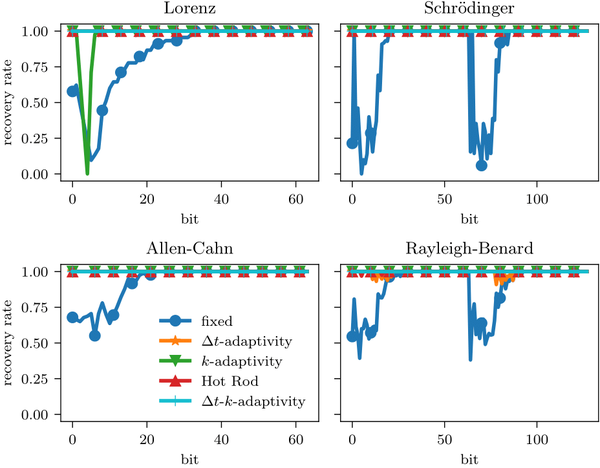
Die Zeitintegrationsmethode Spectral Deferred Correction (SDC) bietet mehrere Formen der Adaptivität, bei der die Genauigkeit gemessen wird und zusätzliche Arbeit geleistet wird, um die Genauigkeit zu erhöhen, wenn die Zielvorgabe nicht erreicht wird. Dies ist in erster Linie eine Strategie zur Anpassung der zeitlichen Auflösung an die Anforderungen des Problems zur Laufzeit. Wenn jedoch das Genauigkeitsziel aufgrund eines temporären Fehlers, der die Lösung verändert, nicht erreicht wird, wird die adaptive SDC auch mehr Arbeit aufwenden, um den Fehler zu korrigieren. Wir zeigen, dass Adaptivität die Recheneffizienz und gleichzeitig die Widerstandsfähigkeit gegenüber weichen Fehlern für eine Reihe von Problemen erhöhen kann, indem wir Experimente mit dem manuellen Einfügen von Bitflips in die Lösung durchführen.

_{Ref. Thomas Baumann, Sebastian Götschel, Thibaut Lunet, Daniel Ruprecht, Robert Speck, Resilience Against Soft Faults through Adaptivity in Spectral Deferred Correction, arXiv.2412.00529 [cs.DC], submitted.}