Colloids
Colloidal rods in shear flow

Colloids with an anisotropic elongated shape, rods, are one of the typical building blocks of a large family of systems known as liquid crystals. Liquid crystals have found a large number of technical applications due to their versatility and rich phase behavior.
Suspensions of rod-like colloids show in equilibrium an isotropic-nematic coexistence region. The location and width of this region depends on the strength of the attraction interaction between rods. By means of hydrodynamic simulations we study the behavior of this phase transition in shear flow.
The shear flow induces alignment in the initially isotropic phase, which narrows the phase coexistence region. A collective rotational motion is induced in the originally nematic phase. This effect contributes to maintain the phase separation. A combined simulation-experimental study shows the existence of a universal shape of the non-equilibrium phase diagram.
Small Spherical Particles in a Polymer Solution

The depletion interaction between colloidal particles and nonadsorbing polymer chains has mainly been studied for large particle size and is less understood in the so-called protein-limit of small particle size. At a first glance this interesting case looks complicated since it is dominated by configurations with the chain coiling around the particle and approximations treating the chain as nondeformable fail completely. However, on relating it via the polymer-magnet analogy to a field theory at the critical point, exact results can be achieved for the monomer-density distribution around one and two small particles.
Polymer Depletion and Potential of Mean Force between a Colloidal Particle and a Wall
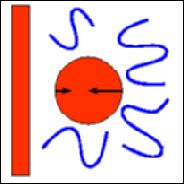
One of the basic interactions in colloid physics is the force induced between colloidal particles or a particle and a wall by adding nonadsorbing free polymer chains. For entropic reasons the chains avoid the space between the particle and the wall leading to an unbalanced pressure which pushes the particle towards the wall. We find that the particle-wall interaction crucially depends on the particle-to-polymer size ratio p: While for large p the force decreases monotonically with increasing distance between particle and wall,for small p the force displays a maximum.
