Excitations
Temperature and bath size in exact diagonalization dynamical mean field theory
Dynamical mean field theory is one of the key methods to describe electronic properties of strongly correlated materials. If exact diagonalization is used as impurity solver, the size of the finite bath representing the infinite lattice is limited because of the rapid growth of the Hilbert space. In view of the increasing interest in the effect of multi-orbital and multi-site Coulomb correlations in transition metal oxides, high-Tc cuprates, iron-based pnictides, organic crystals, etc., it is appropriate to explore the range of temperatures and bath sizes in which exact diagonalization provides accurate results for various system properties. On the one hand, the bath must be large enough to achieve a sufficiently dense level spacing, so that useful spectral information can be derived, especially close to the Fermi-level. On the other hand, for an adequate projection of the lattice Green's function onto a finite bath, the choice of the temperature is crucial. The role of these two key ingredients in exact diagonalization DMFT is discussed for a wide variety of systems in order to establish the domain of applicability of this approach. Three criteria are used to illustrate the accuracy of the results: (i) the convergence of the self-energy with bath size, (ii) quality of the discretization of the bath Green's function, and (iii) comparisons with complementary results obtained via continuous-time quantum Monte Carlo DMFT. The materials comprise a variety of multi-orbital systems, as well as single-band Hubbard models for two-dimensional triangular, square and honeycomb lattices, where non-local Coulomb correlations are important. The main conclusion from these examples is that a larger number of correlated orbitals or sites requires a smaller number of bath levels. Down to temperatures of 5 to 10 meV two bath levels per correlated impurity orbital or site are usually adequate.
(A. Liebsch, H. Ishida) Topical Review: J. Phys. CM 24, 053201 (2012)
Correlated Dirac fermions on the honeycomb lattice studied within cluster dynamical mean field theory

The role of nonlocal Coulomb correlations in the honeycomb lattice is investigated within cluster dynamical mean field theory combined with finite-temperature exact diagonalization. The paramagnetic semimetal-to-insulator transition is found to be in excellent agreement with finite-size determinantal quantum Monte Carlo simulations and with cluster dynamical mean field calculations based on the continuous-time quantum Monte Carlo approach. As expected, the critical Coulomb energy is much lower than within a local or single-site formulation. Short-range correlations are shown to give rise to a pseudogap and concomitant non-Fermi-liquid behavior within a narrow range below the Mott transition.
(A. Liebsch) Phys. Rev. B 83, 035113 (2011)
High-energy pseudogap in iron pnictides induced via Hund coupling
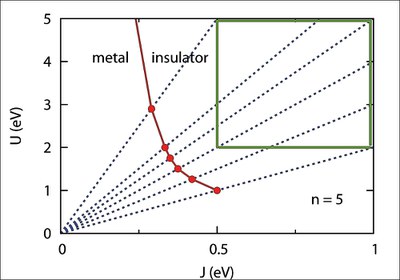
The discovery of superconductivity in iron pnictides has stimulated intense discussions concerning the role of correlation effects, in particular, the importance of Hund exchange interactions. Optical data reveal a high-energy pseudogap not compatible with normal metal behavior. This pseudogap differs fundamentally from the low-energy gap in the antiferromagnetic spin-density wave phase. To analyze the effect of Hund coupling, the degenerate five-band Hubbard model is studied within dynamical mean field theory combined with exact diagonalization. A significant depletion of spectral weight is found above the Fermi level. It is shown that this pseudogap is associated with a collective mode in the self-energy caused by spin fluctuations. The pseudogap is remarkably stable over a wide range of Coulomb and exchange energies, but disappears for weak Hund coupling.
(A. Liebsch) Phys. Rev. B 84, 180505 (2011) (Rapid Communication)
Coulomb blockade and Kondo effect in the electronic structure of Hubbard molecules linked between metal leads

The electronic structure of small Hubbard molecules coupled between two non-interacting semi-infinite leads is studied in the low bias-voltage limit. To calculate the finite-temperature Green's function of the system, each semi-infinite lead is simulated by a small cluster, so that the problem is reduced to that of a finite-size system comprising the molecule and clusters on both sides. The Hamiltonian parameters of the cluster is chosen such that its embedding potential coincides with those of the semi-infinite leads on Matsubara points. Exact diagonalization based on the Arnoldi approach is used to evaluate the effect of Coulomb correlations on the electronic properties of the molecule at finite temperature. Depending on important Hamiltonian parameters, such as Coulomb repulsion and one-electron hopping within the molecule, and hybridization between molecule and leads, the self-energy of the molecule is shown to exhibit standard Fermi-liquid behavior or non-Fermi-liquid-like deviations giving rise to finite electronic scattering rates. The present method can also describe the formation of Kondo resonances inside correlation-induced pseudogaps, as far as the associated Kondo temperature is comparable with the temperature range studied by the exact diagonalization, whose lower boundary can be reduced by increasing the cluster size. These results demonstrate how the system can be tuned between the ballistic transport regime, the Coulomb blockade regime, and the Kondo regime.
(H. Ishida, A. Liebsch) Rhys. Rev. B 86, xxx (2012)
Spin excitations in nanostructures
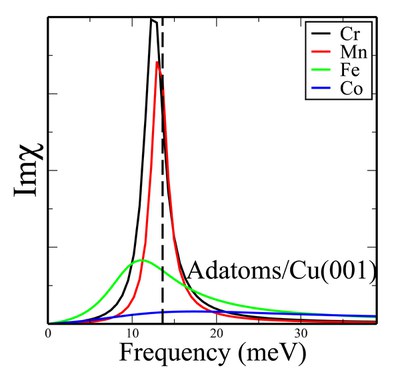
Besides ground state properties, it is possible nowadays to grasp information on the magnetic excitations of nanostructures (adatoms, clusters and thin films) with state of the art inelastic scanning tunneling spectroscopy or electron energy loss spectroscopy. The theoretical investigation of these excitations hinges on the ability to access quantum mechanical processes behind the dynamics of a system. We use time dependent density functional theory combined with the Korringa-Kohn-Rostoker Green function method to devise a real-space scheme that enables the description of the main characteristics of magnetic excitations, i.e. their resonance frequency, their lifetime and their behavior upon application of external perturbations.
More details: Funsilab
Doppel- und Ladungstransferanregungen
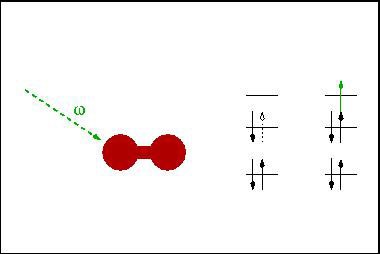
In the endeavor for an ab initio understanding of the electronic structures of complex physical systems, double and charge transfer excitations are both receiving increasing attention due to their possible technological relevance. The former are involved in many ultra-fast processes which are now experimentally accessible while the latter are believed to be essential in explaining complex processes involved in photosynthesis. The challenges to describe double and charge-transfer excitations within a density-functional framework are related since both require a functional which is non-local in space and time. Especially the non-locality in time, i.e. a frequency
dependence, is missing from currently available functionals.
We want to develop a frequency-dependent density functional which will enable us to describe both double and charge-transfer excitations. Moreover, as an alternative approach we will employ reduced density-matrix functional theory, which has proven to be capable of solving many long-standing problems in density-functional theory. We will provide a stringent derivation of a time dependent version of reduced density-matrix functional theory and derive a functional of the density matrix appropriate for the description of charge-transfer and double excitations. The properties of all functionals will be derived from exact calculations for one and two-dimensional model systems where the interacting Schrödinger equation can be solved without approximations for a small number of particles.
Wir wollen ein frequenzabhängiges Dichtefunktional entwickeln, das uns die Beschreibung von Doppel- und Ladungstransferanregungen ermöglicht. Als alternative Methode werden wir reduzierte Dichtematrix-Funktionaltheorie einsetzen, die unter Beweis gestellt hat, viele hartnäckige Probleme der Dichtefunktionaltheorie lösen zu können. Wir werden zunächst die zeitabhängigen Version von reduzierter Dichtematrix-Funktionaltheorie formal korrekt herleiten und darauf aufbauend ein Funktional der reduzierten Dichtematrix ableiten, das für die Beschreibung von Doppel- und Ladunstransferanregungen geeignet ist. Die Eigenschaften aller Funktionale werden aus exakten Rechnungen für ein- bzw. zweidimensionale
Modellsysteme hergeleitet, für die eine Lösung der Schrödingergleichung ohne zusätzliche Näherungen für eine kleine Teilchenzahl möglich ist.
Many-Body Perturbation Theory and the GW Approximation
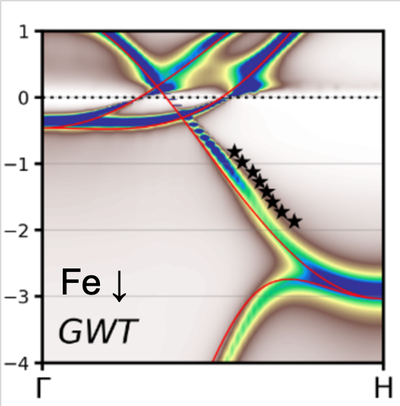
While density-functional theory is an efficient ground-state scheme, many-body perturbation theory gives access to excited states and is thus the method of choice to calculate accurate excitation energies and spectroscopic functions. It is based on Green function techniques and an expansion of correlation functions in terms of Feynman diagrams. The most important practical realization is the GW approximation for the electronic self-energy, which significantly improves the description of quasiparticle band structures, but it can equally be used to study exciton and magnon resonances in density and spin susceptibility. Our implementation in the program SPEX is based on the full-potential linearized augmented plane-wave (FLAPW) approach, along with FLEUR. The contribution from core electrons, the spin polarization of magnetic materials, as well as relativistic effects including spin-orbit coupling can be taken into account. It is also possible to extend the self-energy to include electron-magnon scattering effects. This combined GWT self-energy gives rise to strong lifetime effects and band anomalies, as is shown in the figure for bulk iron.
