Time parallelization across the steps

The past decade has seen a growing interest in the development of parallel methods for temporal integration of ordinary differential equations (ODEs), particularly in the context of temporal strategies for partial differential equations (PDEs). One factor fueling this interest is related to the evolution of supercomputers during this time. To obtain large-scale parallelization in time, various methods such as Parareal, diagonalization or the parallel full approximation scheme in space and time (PFASST) can be used to integrate multiple time steps simultaneously.

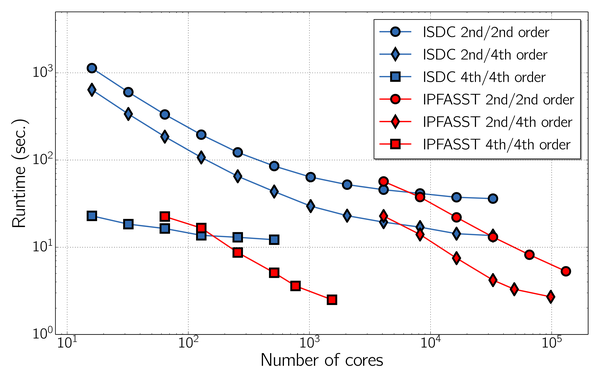
PFASST

To overcome the inherent serial dependence in the time direction, PFASST introduces a space-time hierarchy, where integrators with different costs are coupled in an iterative fashion. Serial dependencies are shifted to the coarsest level, allowing the computationally expensive parts on finer levels to be treated in parallel. This method shows a strong relationship to linear or nonlinear multigrid methods and can be analyzed in a similar way.
_{Ref: M. L. Minion, R. Speck, M. Bolten, M. Emmett, and D. Ruprecht, Interweaving PFASST and Parallel Multigrid, SIAM Journal on Scientific Computing, 37(5), 244 - 263, 2015.}

Diagonalization

In order to avoid coarsening with all its pitfalls, diagonalization-based methods make use of block-circulant preconditioners to parallelize the integration of multiple time-steps. These preconditioners can be diagonalized efficiently using Fast Fourier Transformations (FFT) in time and while this approach works well even for hyperbolic problems, its direct application is restricted to linear problems. The key question addressed in this field of research is how to obtain efficient parallel integrators for nonlinear problems.
_{Ref: Gayatri Caklovic, Robert Speck, Martin Frank, A parallel implementation of a diagonalization-based parallel-in-time integrator, arXiv:2103.12571 [math.NA], submitted.}

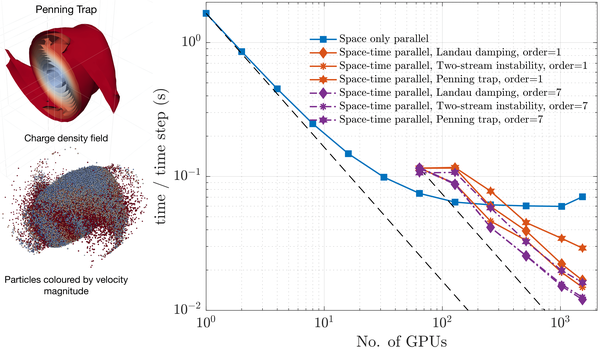
Parareal for particle-mesh methods

Kinetic plasma simulations involve simulating a high -dimensional PDE and particle-mesh methods are the preferred methods for it. They typically need integrating over hundreds of thousands of time steps in a long time interval. In this research we accelerate kinetic plasma simulations by time parallelizing the particle-in-Fourier schemes using the parareal algorithm. The key question we try to explore is how time parallelization can be applied to complex, nonlinear, high-dimensional coupled system of PDEs with wide range of spatial and temporal scales.
_{Ref: Sriramkrishnan Muralikrishnan, Robert Speck, ParaPIF: A Parareal Approach for Parallel-in-Time Integration of Particle-in-Fourier schemes, arXiv:2407.0085 [math.NA], submitted.}