Time parallelization across the method

If the application of high-order, multi-stage time integrators is possible or even required, another way to introduce parallelization in time is the usage of stage-parallel integrators. While the potential for parallelism is naturally limited here, the implementation is rather straightforward and the efficiency is usually favorable. Yet, finding good stage-parallel methods is the major challenge. The group primarily focuses on spectral deferred corrections (SDC) with parallel preconditioners. Both artificial and natural intelligence can be helpful ingredients here.

PFASST-ER

In this work we couple PFASST with a parallel spectral deferred correction (SDC) method, forming an unprecedented doubly time-parallel integrator. While PFASST provides global, large-scale “parallelization across the steps”, the inner parallel SDC method also allows integrating each individual time-step “parallel across the method” using a diagonalized local Quasi-Newton solver. This new method, which we call “PFASST with Enhanced concuRrency” (PFASST-ER), therefore exposes even more temporal concurrency.
_{Ref: Schöbel, R., Speck, R. PFASST-ER: combining the parallel full approximation scheme in space and time with parallelization across the method. Comput. Visual Sci. 23, 12, 2020.}

Space-time parallel SDC: Gray-Scott equation

These plots show an example where a 3D Gray-Scott reaction diffusion equation is solved using a spectral method in space and diagonal spectral deferred correction (SDC) in time. The Gray-Scott equation exhibits the Turing instability, which leads to the formation of complex tubular networks like in the 3D rendering and in the 2D slice plot. In contrast to many other PinT methods, the parallel-across-the-method algorithm diagonal SDC has competitive parallel efficiency to space-parallel methods. Adding diagonal SDC extends the scaling capabilities because the communication workload is shifted from expensive all-to-all operations to cheaper reduce operations, as shown in the scaling plot. This allows to scale to the entire JUWELS Booster GPU machine, whereas spatial parallelism saturates earlier.

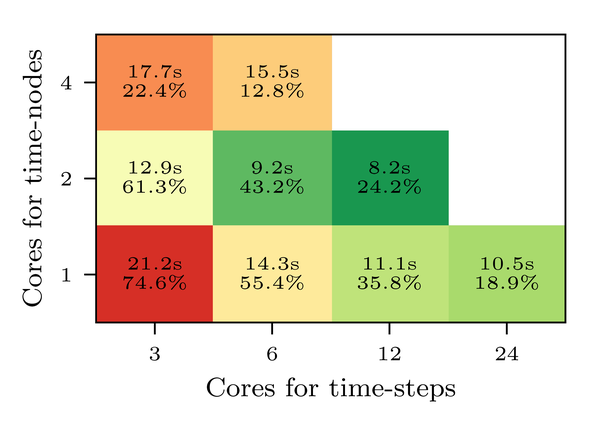
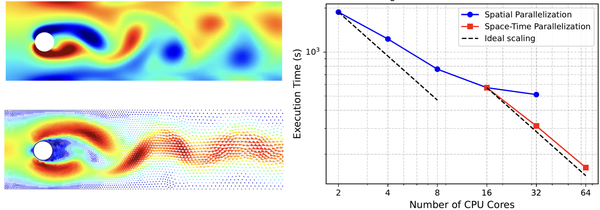
Space-time parallel SDC: Computational Fluid Dynamics

In Computational Fluid Dynamics (CFD), achieving high-fidelity simulations especially in time-sensitive applications, often necessitates fine temporal resolutions, leading to substantial computational demands. One way to achieve temporal parallelization in SDC is through parallelization across the method. The group is investigating the use of parallel SDC methods to enable both space and time parallelization for CFD problems.