ChASE - Chebyshev Accelerated Subspace Eigensolver

The Chebyshev Accelerated Subspace Eigensolver (ChASE) is a modern and scalable library to solve dense Hermitian (Symmetric) algebraic eigenvalue problems of the form

𝐴 𝑥̂ = 𝜆 𝑥̂  with 𝐴^† = 𝐴 ∈ ℂ^𝑛×𝑛 (𝐴^𝑇 = 𝐴 ∈ ℝ^𝑛×𝑛),

where 𝑥̂ ∈ ℂ^𝑛∖{0} and 𝜆 ∈ ℝ are the eigenvector and the eigenvalue of 𝐴, respectively. The ChASE library is based on one of the oldest iterative algorithms dating back to the late 1960s. The current algorithm, visualized below, has at its core a spectral filter powered by Chebyshev polynomials that makes the eigensolver both powerful and very efficient from the performance point of view.

Algorithm

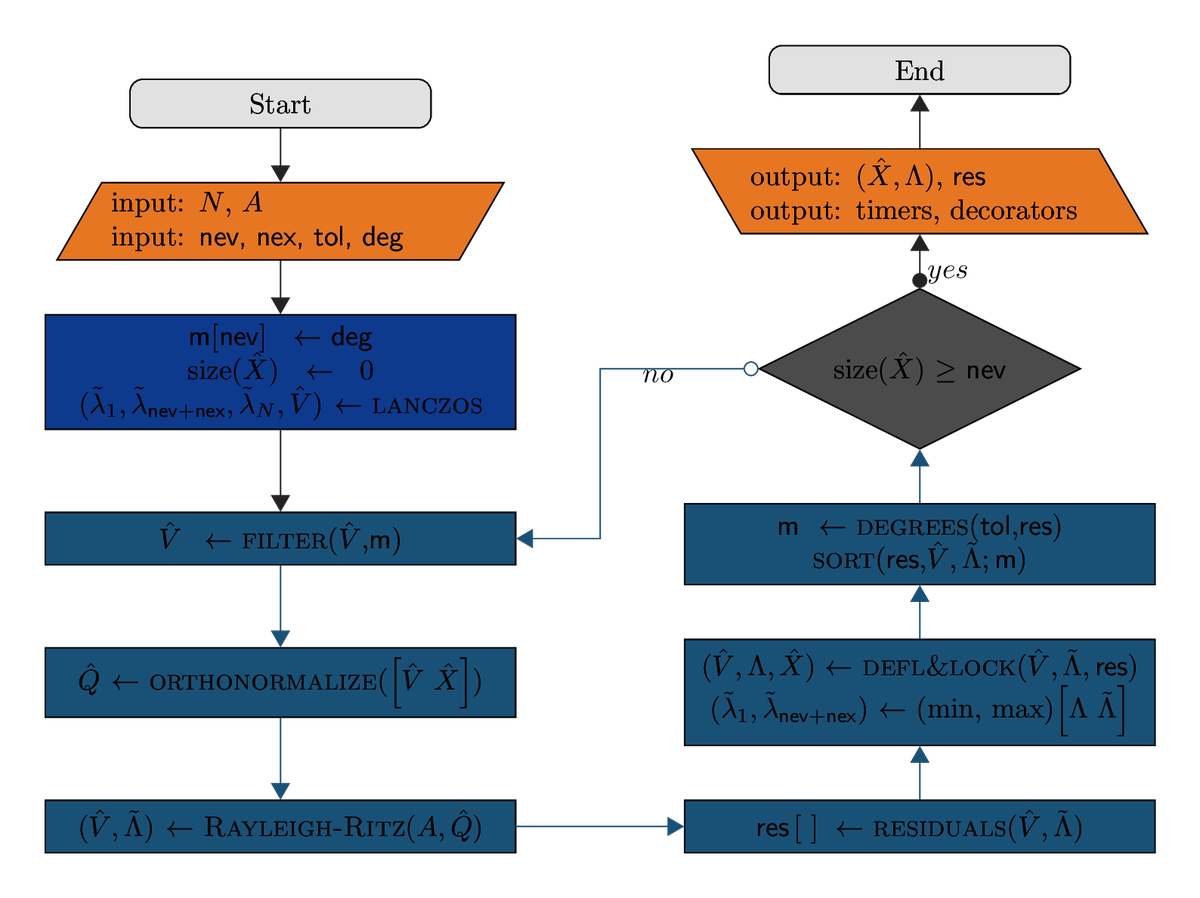
The ChASE library is fully parallelized, it includes an optimization algorithm to compuyte the best polynomial degree towrds convergence, and is particularly effective for sequences of eigenproblems as often arise in electronic structure theory. The main use cases and features of the library are:

Real and Complex: ChASE is templated for real and complex numbers. So it can be used to solve real symmetric eigenproblems as well as complex Hermitian ones.

Eigespectrum: ChASE algorithm is designed to solve for the extremal portion of the eigenspectrum (i.e., {𝜆1,…,𝜆𝗇𝖾𝗏}). By default it computes the lowest portion of the spectrum but it can compute as well the largest portion by solving for −𝐴
The library is particularly efficient when no more than 20% of the extremal portion of the eigenspectrum is sought after. For larger fractions the subspace iteration algorithm may struggle to be competitive. Converge could become an issue for fractions close to or larger than 50%.

Type of Problem: ChASE can currently handle only standard eigenvalue problems. Generalized eigenvalue problems of the form 𝐴𝑥̂  = 𝜆𝐵𝑥̂ , with 𝐵 s.p.d., can be solved after factorizing 𝐵 = 𝐿𝐿^𝑇 and transforming the problem into standard form 𝐴 = 𝐿⁻¹𝐴𝐿^−𝑇.

Sequences: ChASE is particularly efficient when dealing with sequences of eigenvalue problems, where the eigenvectors solving for one problem can be use as input to accelerate the solution of the next one.

Vectors input: Since it is based on subspace iteration, ChASE can receive as input a matrix of vector V  equal to the number of desired eigenvalues. ChASE can experience substantial speed-ups when V contains some information about the sought after eigenvectors.

Degree optimization: For a fixed accuracy level, ChASE can optimize the degree of the Chebyshev polynomial filter so as to minimize the number of FLOPs necessary to reach convergence.

Precision: ChASE is also templated to work in Single Precision (SP) or Double Precision (DP).

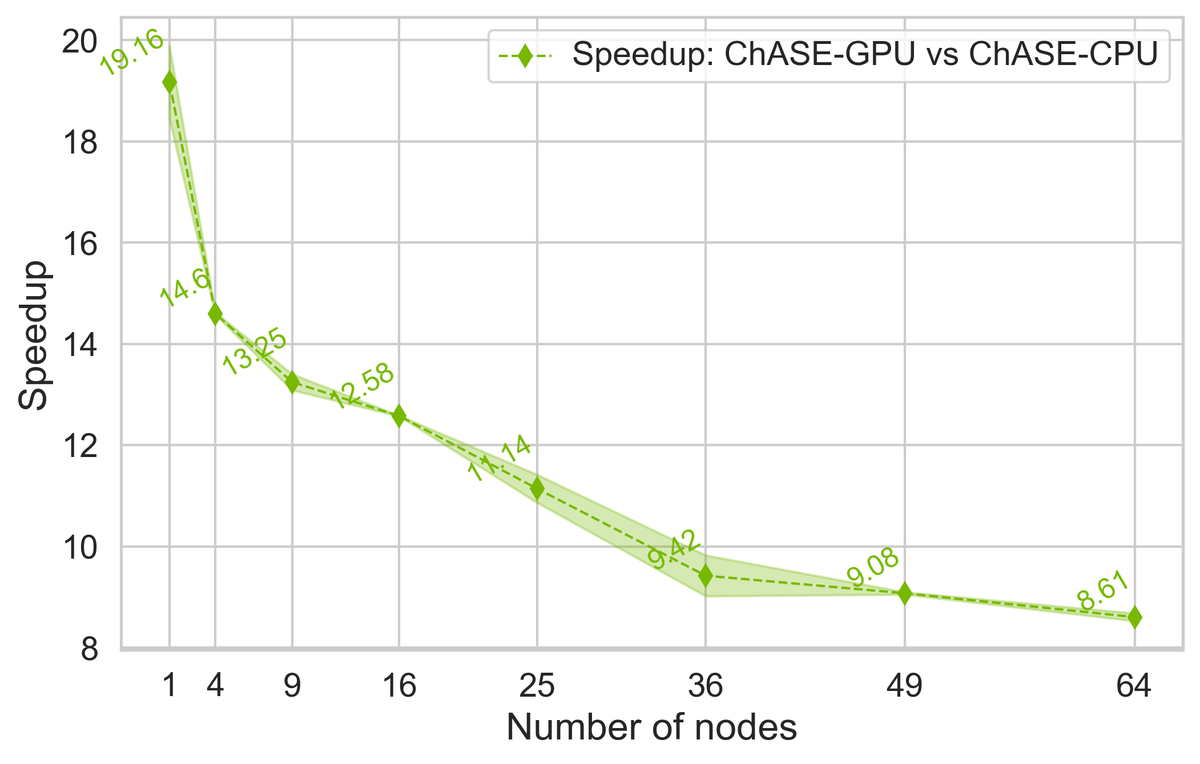
Platform: ChASE is fully parallelized and can be built for both distributed CPU and distributed multi-GPU architectures. The GPU build achieves at least more than 8X speed-up with respect to the pure CPU build on our in-house JUWELS booster.