Benchmarking and prototype applications

Benchmarking

Current quantum devices vary in architecture and device quality. Proper benchmarking is necessary to objectively judge their performance. Bechmarking can be conducted in different ways: hardware-close benchmarking, such as evaluating gate fidelity, read-out noise, compiler performance, and connectivity. A further approach is to implement and execute generic (easy) algorithms and use cases whose results will affected by all error sources and their interdependencies. The latter approach benchmarks the system as a whole and considers how the combination of all error sources affects the accuracy of the solution, i.e. the sequence of physical manipulation of the system, rather than focusing only on the individual error sources omitting the question of how they propagate through an algorithm.

A generic algorithm is for example the variational quantum eigensolver, which combines (variationally) quantum and classical computation. It is based on the search of the ground-state energy of a Hamiltonian, i.e. the smallest eigenvalue (-> eigensolver). A special VQE is the so called quantum approximate optimization algorithm that produces approximate solutions for combinatorial optimization problems. The core of VQEs is splitting the algorithm into two parts: the first part, the energy sampling is performed on a quantum device. The second part, processed on a classical machine, optimizes those parameters which are used to approximate the minimum energy.

Read more:

Farhi, E., Goldstone, J., Gutmann, S., A Quantum Approximate Optimization Algorithm, 2014 https://doi.org/10.48550/arXiv.1411.4028

Moll, N., Barkoutsos, P., Bishop, L. S., Chow, J. M., Cross, A., Egger, D. J., Filipp, S., Fuhrer, A., Gambetta, J. M., Ganzhorn, M., Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol., 3, 3 (2018) https://doi.org/10.1088/2058-9565/aab822.

Prototype applications

Identifying and developing use cases and prototype applications are an indispensable basis for solving large-scale problems in the future. Only the ability to solve “real-world” problems will shift quantum computing from being an academic exercise towards representing a disruptive technology that impacts our daily life. Currently, the community explores new areas of applications and designs small-scale prototype applications to assess the potential of quantum computers. It is key to understanding how to formulate and solvesuch problems on a quantum computer. Moreover, relevant prototype applications might require certain hardware designs. They may thus directly impact which kinds of quantum computers will be used and how they must be designed to produce useful solutions. Implementing prototype applications is also an implicit way of benchmarking that investigates the problem-specific performance as a whole without explicitly investigating typical measures such as fidelity and coherence times.

The following use cases represent special small-scale problems, which have the potential to be scaled up to real-world applications. Moreover, the use cases were used to benchmark different quantum devices.

Tail assignment problem – benchmarking and algorithm development

Planning flight schedules is a very large and challenging “real-world”problem that has to be solved regularly by airlines. Airlines must optimize flight routes in such a way that the costs for aircrafts and flight crews are minimized while respecting regulation by aviation authorities. Such problems are called Tail Assignment problems and might be efficiently solvable by quantum computers in the near future. A simplified Tail Assignment problem, consisting of 472 flights between airports so that routes do not overlap, was solved with the Jülich Universal Quantum Computer Simulator (JUQCS). The problem was addressed using the Quantum Approximate Optimization Algorithm (QAOA) with 40 qubits and a unique solution, a flight schedule with 9 routes.

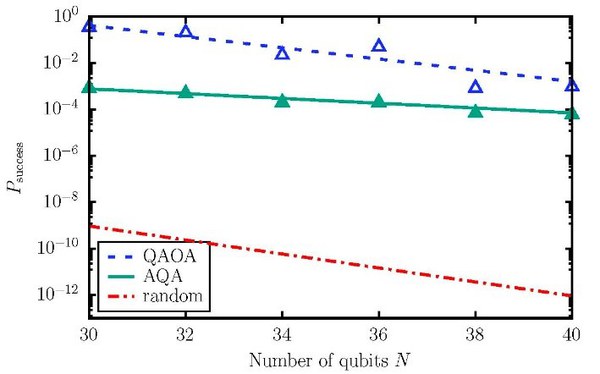
Within this experiment JUQCS was also used to benchmark JUWELS Booster solving several Tail Assignment problems of different sizes with the QAOA and with approximate quantum annealing (AQA), which is a coarse, second-order time-discretization of quantum annealing. Unexpectedly, it was found that AQA performs well compared to the QAOA showing a much weaker decrease of success probability with increasing problem size than the QAOA. Moreover, while the QAOA requires a difficult classical optimization of several variational parameters, AQA only has the time step as a single parameter to optimize. AQA is thus computationally much less intensive. #

Read more:

Willsch, D., Willsch,M., Jin, F.,Michielsen, K., De Raedt, H., GPU-accelerated simulations of quantum annealing and the quantum approximate optimization algorithm, Comput. Phys. Commun. 278, 108411 (2022) https://doi.org/10.1016/j.cpc.2022.108411.

Willsch, D., Willsch, M., Gonzalez Calaza, C.D., Jin, F., De Raedt, H., Svensson, M., Michielsen, K. Benchmarking Advantage and D-Wave 2000Q quantum annealers with exact cover problems, Quantum Inf. Process.
21, 141 (2022) https://doi.org/10.1007/s11128-022-03476-y

Companion planting

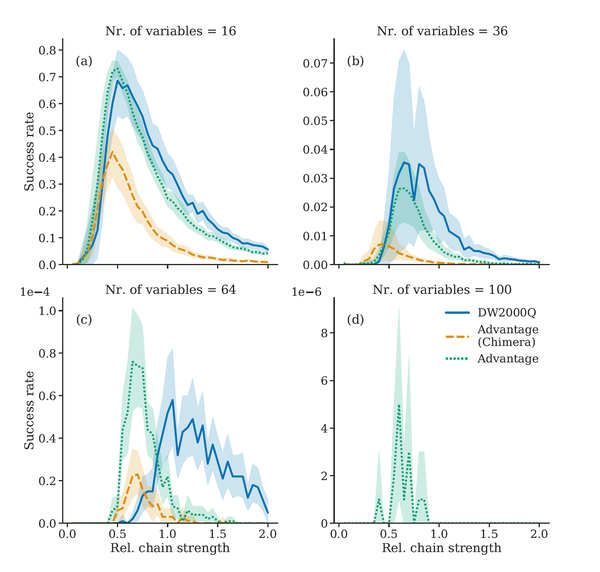
Advancingquantum processing units (QPUs) of quantum annealers requires scalable benchmarking problems to ensure a systematic evaluation of their performance. Such scalable problems can be so called garden optimization problem, which optimize the placement of vegetable plants in the garden, considering favorable, neutral and antagonistic relations between different species. The problem has to be translated to a quadratic unconstrained binary optimization (QUBO) problem with boundary conditions to be solvable by D-Wave’s quantum annealers. A comparison between the 2000+ qubit system D-Wave 2000Q and the 5000+ qubit system D-Wave Advantage revealed that the Advantage system requires less time and exhibits higher success rates, which is what was implicitly expected as the Advantage system is the latest available version. Additionally, it was found that the success rate strongly depends on the embedding of the QUBO problem, which determines how many physical qubits represent one logical qubit (relative chain strength), onto the qubit topology of the systems. With increasing problem size, the maximum of the success rates shifts towards larger relative chain strengths. As the optimal relative chain strength is not automatically chosen by the solvers implemented in the D-Wave systems, it can be beneficial to scan for the optimal chain strength first.

Read more:

Gonzalez Calaza C. D., Willsch D., Michielsen K., Garden optimization problems for benchmarking quantum annealers, Quantum Inf. Process. 20 305 (2021) https://doi.org/10.1007/s11128-021-03226-6

Willsch, D., Willsch, M., Jin, F., Michielsen, K., De Raedt, H., GPU-accelerated simulations of quantum annealing and the quantum approximate optimization algorithm, Comput. Phys. Commun. 278, 108411 (2022) https://doi.org/10.1016/j.cpc.2022.108411

Willsch, D., Willsch, M., Gonzalez Calaza, C.D., Jin, F., De Raedt, H., Svensson, M., Michielsen, K. Benchmarking Advantage and D-Wave 2000Q quantum annealers with exact cover problems, Quantum Inf. Process.
21, 141 (2022) https://doi.org/10.1007/s11128-022-03476-y

Classification in protein-DNA binding

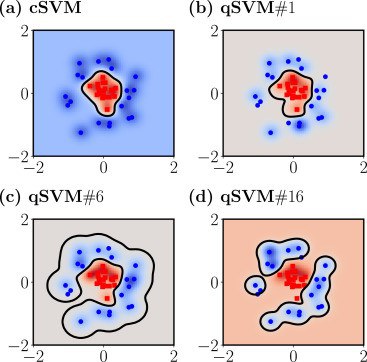
Supervised machine learning algorithms, such as support vector machines (SVM), are popular tools for regression and classification analysis, especially, if the training data set is small. Quantum annealers manufactured by D-Wave System yield various close-to-optimal solutions (qSVM) to a given optimization problem, which leads, in context of machine learning, to multiple classifiers that potentially perform well on unseen data. The results of the qSVM contain a solution which is very similar to the classical SVM but additionally contain solutions that exhibit a more diverse and detailed structure. Moreover, it was found, using real data, that a combination of these quantum-classifiers can improve the classification result compared to classical SVM. The data set contained proteins that show different binding behaviors to a certain DNA sequence. Thus, an ensemble classifier based on qSVM has the potential to generalize better to training data sets and can be helpful for hard problems in the near future if the development of quantum annealers continues with current pace.

Read more:

Willsch, D., Willsch, M., De Raedt, H., Michieslen, K., Support vector machines on the D-Wave quantum annealer, Comput. Phys. Commun. 248, 107006 (2020) https://doi.org/10.1016/j.cpc.2019.107006

Li, R. Y., Di Felice, R., Rohs, R., Lidar, D. A.,Quantum annealing versus classical machine learning applied to a simplified computational biology problem, npj Quantum Inf. 4, 14 (2018) https://doi.org/10.1038/s41534-018-0060-8