Theorie elektrokatalytischer Grenzflächen
Über
Wir entwickeln physikbasierte Modelle für Grenzflächen und Reaktionen in der Elektrokatalyse. Wir verfolgen einen hierarchischen Ansatz für diese komplexen Probleme, indem wir grundlegende Gleichungen (first principles), Modell-Hamiltonianer und phänomenologische Theorien kombinieren.
Unser Ziel | Unsere Standpunkte
Gefördert durch: Helmholtz Investigator Group
"Insight must precede application"
(Max Planck, 1858 - 1947)
Unser Ziel
Entwicklung von konzeptionellen Modellen und theoretischen Instrumenten zum besseren Verständnis von Grenzflächenstrukturen und -prozessen in der Elektrochemie.
Unsere Standpunkte
In einer Zeit, in der die Datenwissenschaft und das maschinelle Lernen eine große Rolle spielen, hat unser fester Glaube an die Leistungsfähigkeit der physikalischen Modellierung unseren Weg bestimmt. Wir stehen fest zu dem immensen Wert, den ein analytischer Ausdruck bei der Entschlüsselung der grundlegenden Mechanismen hat, die einer Vielzahl von Phänomenen zugrunde liegen.
Beim täglichen Umgang mit Gleichungen und theoretischen Modellen in der Forschung vergessen wir oft, sie wirklich zu verstehen. Wenn wir mit dem Rechnen aufhören und uns die Zeit nehmen, selbst die einfachste Gleichung/das einfachste Modell in unserem Bereich zu überdenken, stellen wir vielleicht fest, dass ihre schlafende Kraft noch darauf wartet, geweckt zu werden, und dass eine vollständige Erkenntnis neue Wege zum Aufbau einer besseren Welt eröffnen kann.
Eine Forschungsarbeit verändert vielleicht nicht das Fachgebiet, aber ich stimme voll und ganz zu, dass sie ein entscheidender Moment in der Laufbahn eines Studenten ist.
Forschungsthemen
Dichte-Potential-Funktional-Theorie
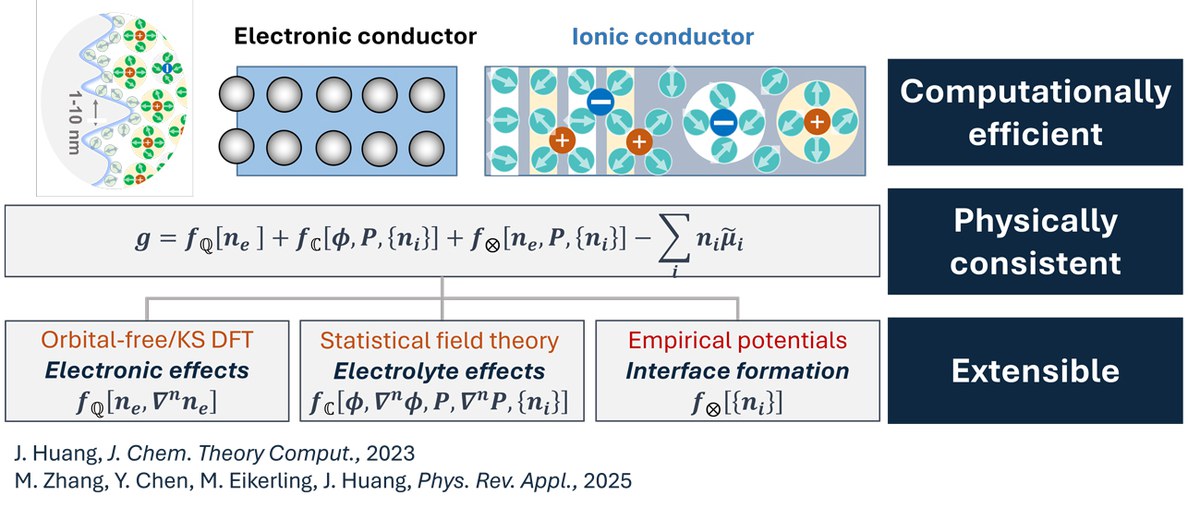
Wir haben einen einzigartigen semiklassischen Funktionsansatz mit konstantem Potential zur Modellierung der elektrischen Doppelschicht (EDL) entwickelt. Unsere Methode kombiniert die orbitalfreie Dichtefunktionaltheorie für Elektronen und die klassische statistische Feldtheorie von Elektrolytlösungen. Unser Ansatz ermöglicht rechnerisch effiziente Simulationen von EDLs unter Konstantpotentialbedingungen und eröffnet einen Weg zur Modellierung von EDLs an aufgerauten Oberflächen und mesoskopischen Strukturen, die jenseits der Möglichkeiten von Ab-Initio-Ansätzen liegen, die durch Rechenkosten und klassische Ansätze ohne Berücksichtigung elektronischer Metalleffekte begrenzt sind.
EDL-Effekte in der Elektrokatalyse
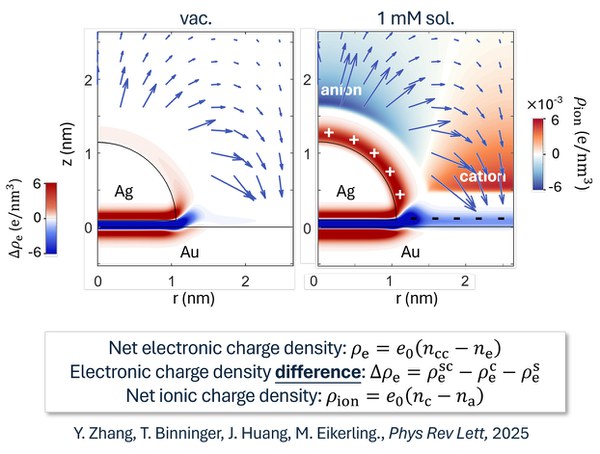
Elektrokatalytische Reaktionen finden in der elektrischen Doppelschicht (EDL) an den Elektroden-Elektrolyt-Grenzflächen statt, wobei der Einfluss der EDL-Struktur auf die Reaktion selbst bei einfachsten Reaktionen unklar ist. Unser Ziel ist es, ein grundlegendes Verständnis der EDL-Effekte auf den elementaren Ladungstransfer an elektrokatalytischen Grenzflächen zu entwickeln, wobei wir das Newns-Anderson-Hamilton-Modell als analytisches Werkzeug verwenden. Der Schwerpunkt liegt dabei auf dem Elektronentransfer an hochgeladenen Elektrodenoberflächen, wie der Ag-Elektrode in der Kohlendioxid-Reduktionsreaktion, für die die klassische Marcus-Theorie unzureichend zu sein scheint.
Heterogene, mesoskopische, dynamische Grenzflächen
In der Praxis sind Elektrokatalysatoren häufig auf mesoskopischer Skala heterogen zusammengesetzt, während die meisten grundlegenden Erkenntnisse über ideal planare Elektroden gesammelt wurden. Ein prominentes Beispiel sind Pt-Nanopartikel auf Kohlenstoffmaterialien, bei denen sich die EDLs von Pt und Kohlenstoff überschneiden. Darüber hinaus sind diese reaktiven Grenzflächen nicht statisch, sondern entwickeln sich während des Betriebs dynamisch weiter. Unser langfristiges Ziel ist es zu verstehen, wie die mesoskopischen Heterogenitäten die EDL-Struktur und die Reaktionskinetik beeinflussen und wie die Reaktionen wiederum die dynamische Entwicklung der Grenzflächen vorantreiben.
"Interest → Preparation → Breakthrough,
I think, is the necessary three-step process for any research work”
(Chen-Ning Yang, 1922-)
Mitglieder
Besucher:innen
Alumni
"Every mathematician has only a few tricks"
(Gian-Carlo Rota, 1932-1999)
Aktivitäten
Informationen von und über die Nachwuchsgruppe
Meldungen
Termine
Veröffentlichungen
Kurse
Professional Service
Teaching and Talks
Letzte Änderung: 21.11.2024